题目内容
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() .
.
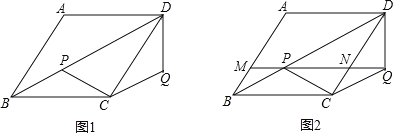
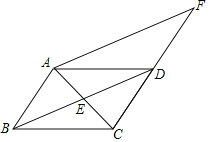
(1)如图1,求证:![]() ;
;
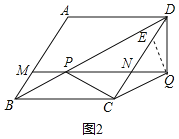
(2)如图2,连接![]() 并延长,分别交
并延长,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
①求证:![]() ;②若
;②若![]() 的最小值为
的最小值为![]() ,直接写出菱形
,直接写出菱形![]() 的面积为 .
的面积为 .
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)由菱形的性质得出BC=DC,∠BCD=120°,由旋转的性质得PC=QC,∠PCQ=120°,得出∠BCP=∠DCQ,由SAS得出△BCP≌△DCQ即可;
(2)①由全等三角形的性质得出BP=DQ,得出∠QDC=∠PBC=∠PBM=30°,在CD上取点E,使QE=QN,则∠QEN=∠QNE,得出∠QED=∠QNC=∠PMB,证明△PBM≌△QDE(AAS),即可得出结论;
②由①知PM=QN,得出MN=PQ=![]() PC,当PC⊥BD时,此时MN最小,则PC=2,BC=2PC=4,菱形ABCD的面积=2△ABC的面积,即可得出答案.
PC,当PC⊥BD时,此时MN最小,则PC=2,BC=2PC=4,菱形ABCD的面积=2△ABC的面积,即可得出答案.
证明:(1)四边形![]() 是菱形,
是菱形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
由旋转的性质得:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,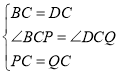 ,
,
![]() ;
;
(2)①证明:由(1)得:![]() ,
,
![]() ,
,
![]() .
.
在![]() 上取点
上取点![]() ,使
,使![]() ,如图2所示:
,如图2所示:
则![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,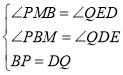 ,
,
![]()
![]() ,
,
![]() .
.
②解:由①知![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 最小,此时
最小,此时![]() 最小,
最小,
则![]() ,
,![]() ,
,
![]() 菱形
菱形![]() 的面积
的面积![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】期中考试中,A,B,C,D,E五位同学的数学、英语成绩有如表信息:
A | B | C | D | E | 平均分 | 中位数 | |
数学 | 71 | 72 | 69 | 68 | 70 |
|
|
英语 | 88 | 82 | 94 | 85 | 76 |
|
|
(1)完成表格中的数据;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩﹣平均成绩)÷成绩方差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?