题目内容
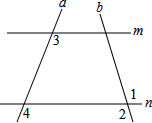 如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空).
如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空).证明:∵∠1=∠2
∴m∥n
∴∠3=∠4
考点:平行线的判定与性质
专题:推理填空题
分析:由已知角相等,利用同位角相等两直线平行得到m与n平行,再利用两直线平行同位角相等即可得证.
解答:证明:∵∠1=∠2(已知),
∴m∥n(同位角相等,两直线平行),
∴∠3=∠4(两直线平行,同位角相等).
故答案为:已知;同位角相等,两直线平行;两直线平行,同位角相等
∴m∥n(同位角相等,两直线平行),
∴∠3=∠4(两直线平行,同位角相等).
故答案为:已知;同位角相等,两直线平行;两直线平行,同位角相等
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若双曲线y=
过两点(-1,y1),(-3,y2),则y1与y2的大小关系为( )
| 2 |
| x |
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、y1与y2大小无法确定 |
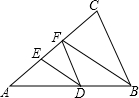 如图,DF∥BC,BF、DE分别平分∠ABC、∠ADF.DE与BF平行吗?为什么?
如图,DF∥BC,BF、DE分别平分∠ABC、∠ADF.DE与BF平行吗?为什么?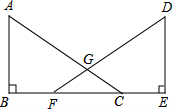 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠BFG=∠ECG.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠BFG=∠ECG. 如图,平行四边形ABCD的面积为
如图,平行四边形ABCD的面积为