题目内容
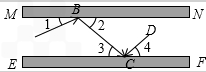
如图,MN、EF分别表示两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?

答案:
解析:
解析:
|
分析:要判断AB与CD的位置关系,应从两直线位置关系的特殊情况入手,如从平行或垂直方面思考问题.观察图形可知,AB与CD没有交点,所以可猜想AB∥CD.要说明AB∥CD,只要说明∠ABC=∠BCD即可. 解:因为MN∥EF, 所以∠2=∠3(两直线平行,内错角相等). 因为∠1=∠2,∠2=∠3,∠3=∠4,所以∠1+∠2=∠3+∠4. 因为∠1+∠ABC+∠2=180°,∠3+∠BCD+∠4=180°, 所以∠ABC=∠BCD. 所以AB∥CD(内错角相等,两直线平行). 点评:这类题型的特点是有条件而无结论,要确定这些条件下可能出现的结论,应从所给的条件出发,通过分析探究,寻求答案. |

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
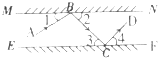 31、如图.MN,EF分别表示两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4.试探索AB和CD间的位置关系,并说明你的理由.
31、如图.MN,EF分别表示两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4.试探索AB和CD间的位置关系,并说明你的理由.
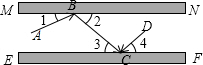 如图.MN,EF分别表示两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4.试探索AB和CD间的位置关系,并说明你的理由.
如图.MN,EF分别表示两面互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的反射光线为CD,此时∠3=∠4.试探索AB和CD间的位置关系,并说明你的理由.