题目内容
(1)如图,A1,A2,A3是抛物线y= x2图象上的三点,若A1,A2,A3三点的横坐标从左至右依次为1,2,3.求△A1A2A3的面积.
x2图象上的三点,若A1,A2,A3三点的横坐标从左至右依次为1,2,3.求△A1A2A3的面积.(2)若将(1)问中的抛物线改为y=
 x2-
x2- x+2和y=ax2+bx+c(a>0),其他条件不变,请分别直接写出两种情况下△A1A2A3的面积.
x+2和y=ax2+bx+c(a>0),其他条件不变,请分别直接写出两种情况下△A1A2A3的面积.(3)现有一抛物线组:y1=
 x2-
x2- x;y2=
x;y2= x2-
x2- x;y3=
x;y3=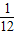 x2-
x2- x;y4=
x;y4= x2-
x2- x;y5=
x;y5=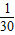 x2-
x2- x;…依据变化规律,请你写出抛物线组第n个式子yn的函数解析式;现在x轴上有三点A(1,0),B(2,0),C(3,0).经过A,B,C向x轴作垂线,分别交抛物线组y1,y2,y3,…,yn于A1,B1,C1;A2,B2,C2;A3,B3,C3;…;An,Bn,Cn.记
x;…依据变化规律,请你写出抛物线组第n个式子yn的函数解析式;现在x轴上有三点A(1,0),B(2,0),C(3,0).经过A,B,C向x轴作垂线,分别交抛物线组y1,y2,y3,…,yn于A1,B1,C1;A2,B2,C2;A3,B3,C3;…;An,Bn,Cn.记 为S1,
为S1,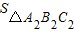 为S2,…,
为S2,…,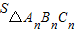 为Sn,试求S1+S2+S3+…+S10的值.
为Sn,试求S1+S2+S3+…+S10的值.(4)在(3)问条件下,当n>10时有Sn-10+Sn-9+Sn-8+…Sn的值不小于
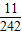 ,请探求此条件下正整数n是否存在最大值?若存在,请求出此值;若不存在,请说明理由.
,请探求此条件下正整数n是否存在最大值?若存在,请求出此值;若不存在,请说明理由.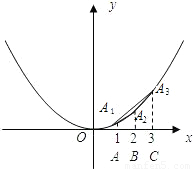
【答案】分析:(1)已知抛物线解析式,求出A1,A2,A3三点的坐标,根据图中几何关系把所求三角形的面积,转化为一个大梯形面积减去两个小梯形的面积,从而求出三角形的面积.第二问与第一问解法一样;
(3)由y1,y2…y5的表达式,归纳出yn的表达式,同时推出面积公式Sn,然后求和.
(4)由(3)的结论,先求和再求n是否存在最大值.
解答:解:(1)∵A1(1, ),A2(2,1),A3(3,
),A2(2,1),A3(3, ),(1分)
),(1分)
∴S△A1A2A3=S梯形A1ACA3-S梯形A1ABA2-S梯形A2BCA3= .
.
(3分)
(2)①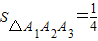 ,(4分)
,(4分)
② .(5分)
.(5分)
(3)由规律知: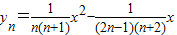 或写成(
或写成( ),(6分)
),(6分)
由(1)(2)知:S1+S2+S3+…+S10= =
= =
= .(8分)
.(8分)
(4)存在,
由上知:Sn-10+Sn-9+Sn-8+…Sn=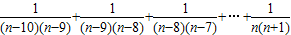 =
= =
=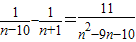 ,(9分)
,(9分)
∵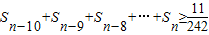
∴ ,
,
∵n>10,
∴n2-9n-10>0,
∴n2-9n-10≤242,(10分)
解得-12≤n≤21,
又∵n>10,
∴10<n≤21,(11分)
∴存在n的最大值,其值为n=21.(12分)
点评:此题是一道规律题,考查抛物线基本性质,巧妙用几何关系,求三角形面积,归纳出规律然后求和,最后一问探究正整数n是否存在最大值,转化为求函数最值问题.
(3)由y1,y2…y5的表达式,归纳出yn的表达式,同时推出面积公式Sn,然后求和.
(4)由(3)的结论,先求和再求n是否存在最大值.
解答:解:(1)∵A1(1,
 ),A2(2,1),A3(3,
),A2(2,1),A3(3, ),(1分)
),(1分)∴S△A1A2A3=S梯形A1ACA3-S梯形A1ABA2-S梯形A2BCA3=
 .
.(3分)
(2)①
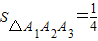 ,(4分)
,(4分)②
 .(5分)
.(5分)(3)由规律知:
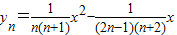 或写成(
或写成( ),(6分)
),(6分)由(1)(2)知:S1+S2+S3+…+S10=
 =
= =
= .(8分)
.(8分)(4)存在,
由上知:Sn-10+Sn-9+Sn-8+…Sn=
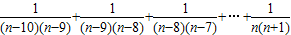 =
= =
=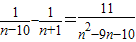 ,(9分)
,(9分)∵
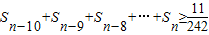
∴
 ,
,∵n>10,
∴n2-9n-10>0,
∴n2-9n-10≤242,(10分)
解得-12≤n≤21,
又∵n>10,
∴10<n≤21,(11分)
∴存在n的最大值,其值为n=21.(12分)
点评:此题是一道规律题,考查抛物线基本性质,巧妙用几何关系,求三角形面积,归纳出规律然后求和,最后一问探究正整数n是否存在最大值,转化为求函数最值问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
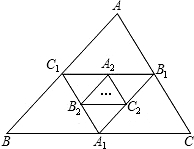 如图:A1,B1,C1分别是BC,AC,AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点…这样延续下去.已知△ABC的周长是1,△A1B1C1的周长是L1,△A2B2C2的周长是L2…AnBnCn的周长是Ln,则Ln=
如图:A1,B1,C1分别是BC,AC,AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点…这样延续下去.已知△ABC的周长是1,△A1B1C1的周长是L1,△A2B2C2的周长是L2…AnBnCn的周长是Ln,则Ln=
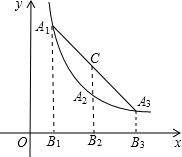 如图,A1、A2、A3是双曲线y=
如图,A1、A2、A3是双曲线y=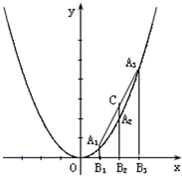 18、如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C,A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为
18、如图,A1、A2、A3是抛物线y=ax2( a>0)上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C,A1、A2、A3三点的横坐标为连续整数n-1、n、n+1,则线段CA2的长为 (2008•淮北模拟)如图,a1,a2,a3,a4的大小关系是( )
(2008•淮北模拟)如图,a1,a2,a3,a4的大小关系是( )