题目内容
 19、在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试(简称初三“一模”)中,九年级某班50名同学选择题(共10小题,每小题3分,满分30分)的得分情况如下表:
19、在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试(简称初三“一模”)中,九年级某班50名同学选择题(共10小题,每小题3分,满分30分)的得分情况如下表:选择题得分分值及人数统计表
| 分 值 | 6 | 12 | 18 | 21 | 24 | 27 | 30 |
| 人 数 | 1 | 2 | 6 | 8 | 15 | 10 | 8 |
0
人;(2)该班选择题得分的平均分为
23.52
,众数为24
,中位数为24
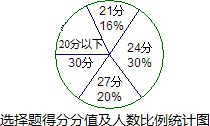
;(3)为了制作右面的扇形统计图(如图),请分别求出得20分以下人数占总人数的百分比及得满分人数的扇形圆心角度数,并补全该扇形统计图.
分析:(1)答对3题得9分,找到得9分的人数即可;
(2)根据平均数,众数和中位数的概念求解即可;
(3)先求出20分以下人数,再求20分以下人数占的比例和圆心角的度数;先求出满分人数,再求满分人数占的比例和圆心角的度数.
(2)根据平均数,众数和中位数的概念求解即可;
(3)先求出20分以下人数,再求20分以下人数占的比例和圆心角的度数;先求出满分人数,再求满分人数占的比例和圆心角的度数.
解答:解:(1)∵得9分的人数为0,
∴该班选择题中,答对3题的人数为0人;
故答案为:0;
(2)平均分为(6×1+12×2+18×6+21×8+24×15+27×10+30×8)÷50=1176÷50=23.52;
24分的人数最多,众数为24;
第25个,第26个的得分都是24,中位数为24.
故答案为:23.52,24,24;
(3)20分以下人数占的比例=(1+2+6)÷50=18%,在扇形统计图中所对的圆心角=360°×18%=64.8°;
满分人数占的比例=8÷50=16%,在扇形统计图中所对的圆心角=360°×16%=57.6°.
∴该班选择题中,答对3题的人数为0人;
故答案为:0;
(2)平均分为(6×1+12×2+18×6+21×8+24×15+27×10+30×8)÷50=1176÷50=23.52;
24分的人数最多,众数为24;
第25个,第26个的得分都是24,中位数为24.
故答案为:23.52,24,24;
(3)20分以下人数占的比例=(1+2+6)÷50=18%,在扇形统计图中所对的圆心角=360°×18%=64.8°;
满分人数占的比例=8÷50=16%,在扇形统计图中所对的圆心角=360°×16%=57.6°.
点评:本题考查平均数、中位数和众数的概念.一组数据的总和除以这组数据个数所得到的商叫这组数据的平均数;在一组数据中出现次数最多的数叫做这组数据的众数;将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.同时考查扇形统计图的制作,在扇形统计图中,每部分占总体的百分比等于该部分所对应的扇形圆心的度数与360°的比.在制作统计图时,要注意写上统计图名称.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试(简称初三“一模”)中,九年级某班50名同学选择题(共10小题,每小题3分,满分30分)的得分情况如下表:
选择题得分分值及人数统计表
| 分 值 | 6 | 12 | 18 | 21 | 24 | 27 | 30 |
| 人 数 | 1 | 2 | 6 | 8 | 15 | 10 | 8 |
(2)该班选择题得分的平均分为______,众数为______,中位数为______;
(3)为了制作右面的扇形统计图(如图),请分别求出得20分以下人数占总人数的百分比及得满分人数
 的扇形圆心角度数,并补全该扇形统计图.
的扇形圆心角度数,并补全该扇形统计图.
在本学期第九周进行的白云区08年初三毕业班中考第一次模拟考试(简称初三“一模”)中,九年级某班50名同学选择题(共10小题,每小题3分,满分30分)的得分情况如下表:
选择题得分分值及人数统计表
(1)该班选择题中,答对3题的人数为______人;
(2)该班选择题得分的平均分为______,众数为______,中位数为______;
(3)为了制作右面的扇形统计图(如图),请分别求出得20分以下人数占总人数的百分比及得满分人数的扇形圆心角度数,并补全该扇形统计图.
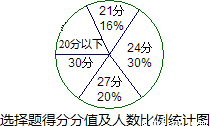
选择题得分分值及人数统计表
| 分 值 | 6 | 12 | 18 | 21 | 24 | 27 | 30 |
| 人 数 | 1 | 2 | 6 | 8 | 15 | 10 | 8 |
(2)该班选择题得分的平均分为______,众数为______,中位数为______;
(3)为了制作右面的扇形统计图(如图),请分别求出得20分以下人数占总人数的百分比及得满分人数的扇形圆心角度数,并补全该扇形统计图.
