题目内容
我们知道:对于任何实数x,
①∵x2≥0,∴x2+1>0;
②∵(x-
)2≥0,∴(x-
)2+
>0.
模仿上述方法解答:
求证:
(1)对于任何实数x,均有:2x2+4x+3>0;
(2)不论x为何实数,多项式3x2-5x-1的值总大于2x2-4x-2的值.
①∵x2≥0,∴x2+1>0;
②∵(x-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
模仿上述方法解答:
求证:
(1)对于任何实数x,均有:2x2+4x+3>0;
(2)不论x为何实数,多项式3x2-5x-1的值总大于2x2-4x-2的值.
分析:(1)将代数式前两项提取2,配方后根据完全平方式为非负数,得到代数式大于等于1,即对于任何实数x,代数式2x2+4x+3的值总大于0,得证.
(2)证明多项式3x2-5x-1的值总大于2x2-4x-2的值时,可以证明3x2-5x-1-(2x2-4x-2)>0
(2)证明多项式3x2-5x-1的值总大于2x2-4x-2的值时,可以证明3x2-5x-1-(2x2-4x-2)>0
解答:证明:(1)∵对于任何实数x,(x+1)2≥0,
∴2x2+4x+3
=2(x2+2x)+3
=2(x2+2x+1)+1
=2(x+1)2+1≥1>0.
(2)∵3x2-5x-1-(2x2-4x-2)
=3x2-5x-1-2x2+4x+2
=x2-x+1
=(x-
)2+
>0
∴多项式3x2-5x-1的值总大于2x2-4x-2的值.
∴2x2+4x+3
=2(x2+2x)+3
=2(x2+2x+1)+1
=2(x+1)2+1≥1>0.
(2)∵3x2-5x-1-(2x2-4x-2)
=3x2-5x-1-2x2+4x+2
=x2-x+1
=(x-
| 1 |
| 2 |
| 3 |
| 4 |
∴多项式3x2-5x-1的值总大于2x2-4x-2的值.
点评:此题考查了配方法的应用,以及非负数的性质:偶次幂,灵活应用完全平方公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,①∵
,①∵ ≥0,∴
≥0,∴ ≥0,∴
≥0,∴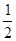 >0.
>0. >0;
>0; 的值总大于
的值总大于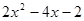 的值.
的值. ,①∵
,①∵ ≥0,∴
≥0,∴ ≥0,∴
≥0,∴ >0.
>0. >0;
>0; 的值总大于
的值总大于 的值.
的值. =(x-1)2+
=(x-1)2+ >0;模仿上述方法解答:
>0;模仿上述方法解答: