题目内容
(2009•永州)如图,在平面直角坐标系中,点A、C的坐标分别为(-1,0)、(0,-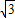 ),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.
),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.(1)求该二次函数的解析式;
(2)若设点P的横坐标为m,用含m的代数式表示线段PF的长;
(3)求△PBC面积的最大值,并求此时点P的坐标.
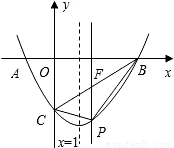
【答案】分析:此题文字比较多,而且图象也比较复杂,所以解题时需要理解题意.
(1)可以采用待定系数法求二次函数的解析式,因为点A(-1,0)、C(0,-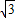 )在函数图象上,对称轴为x=1,也可求得A的对称点B的坐标为(3,0),列方程组即可求得解析式;
)在函数图象上,对称轴为x=1,也可求得A的对称点B的坐标为(3,0),列方程组即可求得解析式;
(2)先求得直线BC的解析式为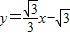 ,则可求得点F的坐标为
,则可求得点F的坐标为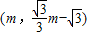 ,再求得点P的纵坐标为
,再求得点P的纵坐标为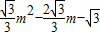 ,可得线段PF的长;
,可得线段PF的长;
(3)利用面积和,△PBC的面积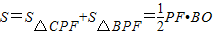 即可求得.
即可求得.
解答:解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c为常数),
由抛物线的对称性知B点坐标为(3,0),
依题意得: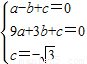 ,(1分)
,(1分)
解得: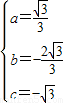 ,(2分)
,(2分)
∴所求二次函数的解析式为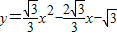 ;(3分)
;(3分)
(2)∵P点的横坐标为m,
∴P点的纵坐标为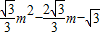 ,(4分)
,(4分)
设直线BC的解析式为y=kx+b(k≠0,k、b是常数),
依题意,得 ,
,
∴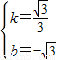 ,
,
故直线BC的解析式为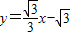 ,(5分)
,(5分)
∴点F的坐标为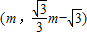 ,
,
∴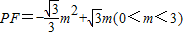 ;(6分)
;(6分)
(3)∵△PBC的面积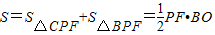 =
=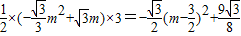 ,
,
∴当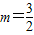 时,△PBC的最大面积为
时,△PBC的最大面积为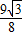 ,(8分)
,(8分)
把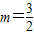 代入
代入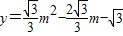 ,
,
得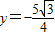 ,
,
∴点P的坐标为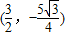 .(10分)
.(10分)
点评:此题考查了学生的综合应用能力,要注意数形结合,认真分析,仔细识图.注意待定系数法求函数的解析式,注意函数交点坐标的求法,注意三角形面积的求法.
(1)可以采用待定系数法求二次函数的解析式,因为点A(-1,0)、C(0,-
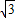 )在函数图象上,对称轴为x=1,也可求得A的对称点B的坐标为(3,0),列方程组即可求得解析式;
)在函数图象上,对称轴为x=1,也可求得A的对称点B的坐标为(3,0),列方程组即可求得解析式;(2)先求得直线BC的解析式为
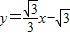 ,则可求得点F的坐标为
,则可求得点F的坐标为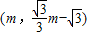 ,再求得点P的纵坐标为
,再求得点P的纵坐标为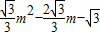 ,可得线段PF的长;
,可得线段PF的长;(3)利用面积和,△PBC的面积
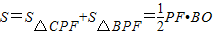 即可求得.
即可求得.解答:解:(1)设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c为常数),
由抛物线的对称性知B点坐标为(3,0),
依题意得:
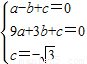 ,(1分)
,(1分)解得:
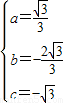 ,(2分)
,(2分)∴所求二次函数的解析式为
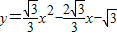 ;(3分)
;(3分)(2)∵P点的横坐标为m,
∴P点的纵坐标为
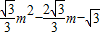 ,(4分)
,(4分)设直线BC的解析式为y=kx+b(k≠0,k、b是常数),
依题意,得
 ,
,∴
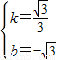 ,
,故直线BC的解析式为
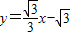 ,(5分)
,(5分)∴点F的坐标为
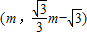 ,
,∴
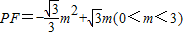 ;(6分)
;(6分)(3)∵△PBC的面积
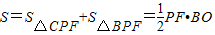 =
=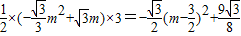 ,
,∴当
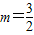 时,△PBC的最大面积为
时,△PBC的最大面积为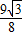 ,(8分)
,(8分)把
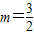 代入
代入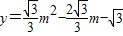 ,
,得
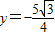 ,
,∴点P的坐标为
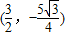 .(10分)
.(10分)点评:此题考查了学生的综合应用能力,要注意数形结合,认真分析,仔细识图.注意待定系数法求函数的解析式,注意函数交点坐标的求法,注意三角形面积的求法.

练习册系列答案
相关题目
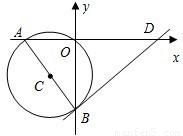
 的⊙C,交y轴的负半轴于点B.
的⊙C,交y轴的负半轴于点B.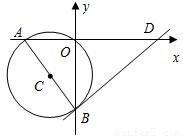
 的⊙C,交y轴的负半轴于点B.
的⊙C,交y轴的负半轴于点B.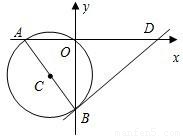
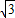 ),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.
),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.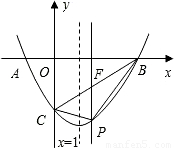
 的⊙C,交y轴的负半轴于点B.
的⊙C,交y轴的负半轴于点B.