题目内容
证明:对任意三角形,一定存在两条边,它们的长u,v满足1≤| u |
| v |
1+
| ||
| 2 |
分析:设任意△ABC的三边长为a,b,c,不妨设a>b>c.若结论不成立,则可证明
和
的取值范围,然后记b=c+s,a=b+t=c+s+t,求得
和
的取值范围,再令x=
,y=
,根据条件证明y<1.
| a |
| b |
| b |
| c |
| c+s+t |
| c+s |
1+
| ||||
1+
|
| s |
| c |
| t |
| c |
解答:证明:设任意△ABC的三边长为a,b,c,不妨设a>b>c.若结论不成立,则必有
≥
①
≥
.②
记b=c+s,a=b+t=c+s+t,显然s,t>0代入得
≥
,
≥
,
令x=
,y=
则
≥
.③
由a<b<c,得c+s+t<c+s+c,即t<c,于是.y=
<1
由②得
=
=1+x≥
,④
由③,④得y≥(
-1)(1+x)≥
•
=1,
此式与y<1矛盾.从而命题得证.
| a |
| b |
1+
| ||
| 2 |
| b |
| c |
1+
| ||
| 2 |
记b=c+s,a=b+t=c+s+t,显然s,t>0代入得
| c+s+t |
| c+s |
1+
| ||
| 2 |
1+
| ||||
1+
|
1+
| ||
| 2 |
令x=
| s |
| c |
| t |
| c |
| 1+x+y |
| 1+x |
1+
| ||
| 2 |
由a<b<c,得c+s+t<c+s+c,即t<c,于是.y=
| t |
| c |
由②得
| b |
| c |
| c+s |
| c |
1+
| ||
| 2 |
由③,④得y≥(
1+
| ||
| 2 |
| ||
| 2 |
1+
| ||
| 2 |
此式与y<1矛盾.从而命题得证.
点评:本题主要考查抽屉原理的知识点,根据假设法证明是解答本题的关键,本题难度较大.

练习册系列答案
相关题目
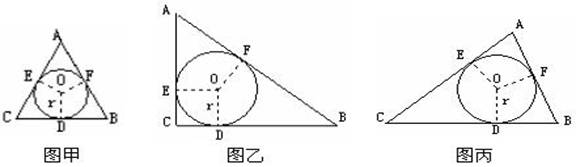
为了探索三角形的内切圆半径r与周长L、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.如图,⊙O是△ABC的内切圆,切点分别为点D、E、F.
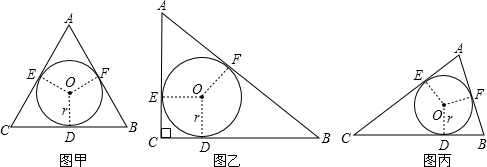
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
(2)观察图形,利用上表实验数据分析、猜测特殊三角形的r与L、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?

(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长L和面积S.(结果精确到0.1厘米)
| AC | BC | AB | r | L | s | |
| 图甲 | 0.6 | |||||
| 图乙 | 5.0 | 1.0 |
(本题满分12分)为了探究三角形的内切圆半径r与周长 、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长 和面积S.(结果精确到0.1厘米)
和面积S.(结果精确到0.1厘米)
(2)观察图形,利用上表实验数据分析.猜测特殊三角形的r与 、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
(3)
 、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长
 和面积S.(结果精确到0.1厘米)
和面积S.(结果精确到0.1厘米)| | AC | BC | AB | r |  | S |
| 图甲 | | | | 0.6 | | |
| 图乙 | | | | 1.0 | | |
 、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?(3)

为了探究三角形的内切圆半径r与周长 、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长 和面积S.(结果精确到0.1厘米)
和面积S.(结果精确到0.1厘米)
|
|
AC |
BC |
AB |
r |
|
S |
|
图甲 |
|
|
|
0.6 |
|
|
|
图乙 |
|
|
|
1.0 |
|
|
(2)观察图形,利用上表实验数据分析.猜测特殊三角形的r与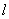 、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
(3)