题目内容
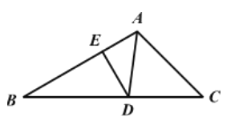
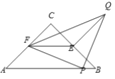
【题目】如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() 与
与![]() 的中点,
的中点,![]() 是
是![]() 上一点,以
上一点,以![]() 为一直角边作等腰直角
为一直角边作等腰直角![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() _________.
_________.
【答案】![]()
【解析】
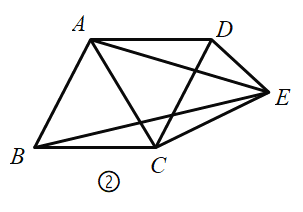
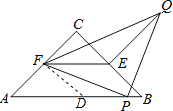
取AB中点D,连接FD,根据等腰直角三角形的性质,由△ABC为等腰直角三角形得到AC=BC=![]() ,∠A=45°,再根据点D、E、F分别是△ABC三边的中点,则AD=BD=4,DP=3,EF为△ABC的中位线,于是可判断△ADF为等腰直角三角形,得到∠FDA=45°,利用三角形中位线的性质得EF∥AB,EF=
,∠A=45°,再根据点D、E、F分别是△ABC三边的中点,则AD=BD=4,DP=3,EF为△ABC的中位线,于是可判断△ADF为等腰直角三角形,得到∠FDA=45°,利用三角形中位线的性质得EF∥AB,EF=![]() AB=4,根据平行线性质得∠EFP+∠DFP=45°;又由于△PQF为等腰直角三角形,则∠EFP+∠EFQ=45°,所以∠DFP=∠EFQ,然后根据有两组对应边成比例且夹角相等的三角形相似,得出△FDP∽△FEQ,再根据相似三角形的对应边成比例即可求得.
AB=4,根据平行线性质得∠EFP+∠DFP=45°;又由于△PQF为等腰直角三角形,则∠EFP+∠EFQ=45°,所以∠DFP=∠EFQ,然后根据有两组对应边成比例且夹角相等的三角形相似,得出△FDP∽△FEQ,再根据相似三角形的对应边成比例即可求得.
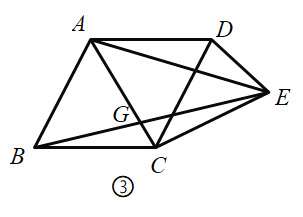
解:取AB中点D,连结FD,D是AB的中点,
如图, ∵△ABC为等腰直角三角形,AB=8,PB=1, ∴AC=BC=![]() ∠A=45°,
∠A=45°,
∵点D、E、F分别是△ABC三边的中点,AB=8,PB=1,
∴AD=BD=4,DP=DB-PB=4-1=3,EF、DF为△ABC的中位线,
∴EF∥AB,EF=![]() AB=4,DF=
AB=4,DF=![]() BC=
BC=![]() ,∠EFP=∠FPD,
,∠EFP=∠FPD,
∴∠FDA=45°,![]()
∴∠DFP+∠DPF=45°,
∵△PQF为等腰直角三角形,
∴∠PFE+∠EFQ=45°,![]()
∴∠DFP=∠EFQ,
∵△PFQ是等腰直角三角形,
∴ ![]() ∴
∴ ![]()
∴△FDP∽△FEQ,
![]() ∴
∴![]()
故答案为:![]()

【题目】为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机拍取40名学生进行问卷调查,其统计结果如表:
最喜欢的线上学习方式(没人最多选一种) | 人数 |
直播 | 10 |
录播 |
|
资源包 | 5 |
线上答疑 | 8 |
合计 | 40 |
(1)![]() ;
;
(2)若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图,求“直播"对应扇形的圆心角度数;
(3)根据调查结果估计该校10000名学生中,最喜欢“线上答疑”的学生人数;
(4)在最喜欢“资源包”的学生中,有2名男生,3名女生.现从这5名学生中随机抽取2名学生介绍学习经验,求恰好抽到1名男生和1名女生的概率.