题目内容
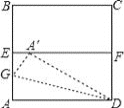
【题目】如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=_________cm.
【答案】4![]() -6.
-6.
【解析】
由ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,可得AE=DF=2cm,EF=AD=4cm,由翻折可得AG=A′G,AD=A′D,在Rt△DFA′与Rt△A′EG中,利用勾股定理可求得答案.
解:∵ABCD是一张边长为4cm的正方形纸片,E、F分别为AB,CD的中点,
∴AE=DF=2cm,EF=AD=4cm,
DG为折痕,
∴AG=A′G,AD=A′D,
Rt△DFA′中,A′F=![]() =
=![]() =2
=2![]() ,
,
∴A′E=4-2![]() ,
,
Rt△A′EG中,设EG=x,则A′G=AG=2-x,
∴![]() ;
;
解得x=4![]() -6.
-6.
故答案为:4![]() -6.
-6.

练习册系列答案
相关题目