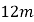题目内容
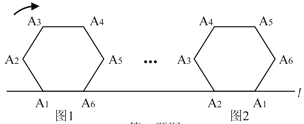
【题目】如图，将边长为
的正六边形A1A2A3A4A5A6在直线
上由图1的位置按顺时针
方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的
长为（ ）．
A. 
B. 
C. 
D. 
【答案】A
【解析】
连A1A5，A1A4，A1A3，作A6C⊥A1A5，利用正六边形的性质分别计算出A1A4=2a，A1A5=A1A3=
a，而当A1第一次滚动到图2位置时，顶点A1所经过的路径分别是以A6，A5，A4，A3，A2为圆心，以a，a，2a，a，a为半径，圆心角都为60°的五条弧，然后根据弧长公式进行计算即可．
解：连A1A5，A1A4，A1A3，作A6C⊥A1A5，如图，
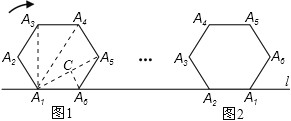
∵六边形A1A2A3A4A5A6为正六边形，
∴A1A4=2a，∠A1A6A5=120°，
∴∠CA1A6=30°，
∴A6C=
a，A1C=
a，
∴A1A5=A1A3=a，
当A1第一次滚动到图2位置时，顶点A1所经过的路径分别是以A6，A5，A4，A3，A2为圆心，
以a，a，2a，a，a为半径，圆心角都为60°的五条弧，
∴顶点A1所经过的路径的长=
+
++，
=
故选A．
练习册系列答案
相关题目
