题目内容
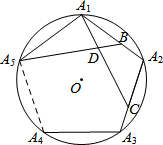（2013•南京二模）如图，点A1、A2、A3、A4、A5在⊙O上，且 |
| A1A2 |
|
| A2A3 |
|
| A3A4 |
|
| A4A5 |
|
| A5A1 |
108°
108°
．分析：首先证明△A1A5B≌△A2A1C，然后依据全等三角形的对应角相等以及三角形的外角的性质，即可证得∠A5DC=∠A5A1A2从而求解．
解答：解：∵
=
=
=
=
，
∴每段弧的度数是：
=72°，
则
的度数是：3×72=216°，
∴∠A5A1A2=108°．
∵在△A1A5B和△A2A1C中，
，
∴△A1A5B≌△A2A1C（SAS），
∴∠A1A5B=∠A2A1C，
∴∠A5DC=∠A1A5D+∠A5A1D=∠A5A1D+∠A2A1C=∠A5A1A2=108°．
故答案是：108°．
|
| A1A2 |
|
| A2A3 |
|
| A3A4 |
|
| A4A5 |
|
| A5A1 |
∴每段弧的度数是：
| 360 |
| 5 |
则
|
| A5A1A2 |
∴∠A5A1A2=108°．
∵在△A1A5B和△A2A1C中，
|
∴△A1A5B≌△A2A1C（SAS），
∴∠A1A5B=∠A2A1C，
∴∠A5DC=∠A1A5D+∠A5A1D=∠A5A1D+∠A2A1C=∠A5A1A2=108°．
故答案是：108°．
点评：本题考查了弧、弦、圆心角的关系，以及全等三角形的判定与性质，正确证明∠A5DC=∠A5A1A2是关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
