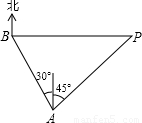
题目内容
一海上巡逻艇在A处巡逻,突然接到上级命令,在北偏西30°方向且距离A处20海里的B港口,有一艘走私艇沿着正东方向以每小时50海里的速度驶向公海,务必进行拦截,巡逻艇马上沿北偏东45°的方向快速追击,恰好在临近公海的私快艇拦截住,如图所示,试求巡逻艇的速度.(结果取整数,参考数据: =1.414,
=1.414,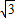 =1.732,
=1.732, =2.499)(提示:过A点作AC垂直BP于C,速度为45海里)
=2.499)(提示:过A点作AC垂直BP于C,速度为45海里)
【答案】分析:本题可通过构建直角三角形来求解.过A点作AC垂直BP于C,那么AC就是直角三角形ABC和ACP的公共直角边,可先求出AC的值,然后求出AP,BP的值.根据BP算出巡逻艇的时间然后根据其路程为AP计算出速度.
解答: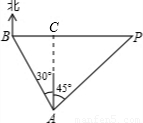 解:过A点作AC垂直BP于C,
解:过A点作AC垂直BP于C,
Rt△ABC中,∠BAC=30°,AB=20,
AC=AB•cos30°=10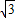 ,
,
BC=AB•sin30°=10,
Rt△ACP中,∠PAC=45°,
AP=AC÷cos45°=10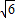 ≈24.99,
≈24.99,
PC=AC=10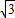 ,
,
∴BP=PC+BC=10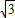 +10≈27.32.
+10≈27.32.
因此巡逻艇用的时间是:27.32÷50=0.5464小时.
巡逻艇的速度是:24.99÷0.5464≈46海里/时.
点评:本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.有公共直角边的先求这条直角边.
解答:
 解:过A点作AC垂直BP于C,
解:过A点作AC垂直BP于C,Rt△ABC中,∠BAC=30°,AB=20,
AC=AB•cos30°=10
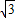 ,
,BC=AB•sin30°=10,
Rt△ACP中,∠PAC=45°,
AP=AC÷cos45°=10
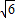 ≈24.99,
≈24.99,PC=AC=10
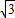 ,
,∴BP=PC+BC=10
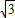 +10≈27.32.
+10≈27.32.因此巡逻艇用的时间是:27.32÷50=0.5464小时.
巡逻艇的速度是:24.99÷0.5464≈46海里/时.
点评:本题是将实际问题转化为直角三角形中的数学问题,可把条件和问题放到直角三角形中,进行解决.有公共直角边的先求这条直角边.

练习册系列答案
相关题目
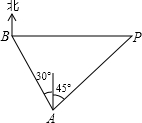 一海上巡逻艇在A处巡逻,突然接到上级命令,在北偏西30°方向且距离A处20海里的B港口,有一艘走私艇沿着正东方向以每小时50海里的速度驶向公海,务必进行拦截,巡逻艇马上沿北偏东45°的方向快速追击,恰好在临近公海的私快艇拦截住,如图所示,试求巡逻艇的速度.(结果取整数,参考数据:
一海上巡逻艇在A处巡逻,突然接到上级命令,在北偏西30°方向且距离A处20海里的B港口,有一艘走私艇沿着正东方向以每小时50海里的速度驶向公海,务必进行拦截,巡逻艇马上沿北偏东45°的方向快速追击,恰好在临近公海的私快艇拦截住,如图所示,试求巡逻艇的速度.(结果取整数,参考数据: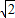 =1.414,
=1.414,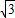 =1.732,
=1.732, =2.449)(提示:过A点作AC垂直BP于C,速度为45海里)
=2.449)(提示:过A点作AC垂直BP于C,速度为45海里)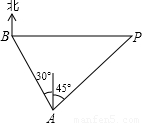
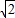 =1.414,
=1.414,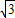 =1.732,
=1.732,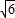 =2.499)(提示:过A点作AC垂直BP于C,速度为45海里)
=2.499)(提示:过A点作AC垂直BP于C,速度为45海里)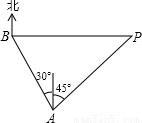
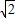 =1.414,
=1.414,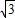 =1.732,
=1.732,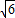 =2.499)(提示:过A点作AC垂直BP于C,速度为45海里)
=2.499)(提示:过A点作AC垂直BP于C,速度为45海里)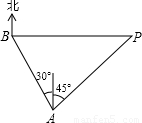
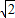 =1.414,
=1.414, =1.732,
=1.732,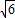 =2.499)(提示:过A点作AC垂直BP于C,速度为45海里)
=2.499)(提示:过A点作AC垂直BP于C,速度为45海里)