题目内容
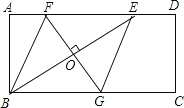
【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=![]() AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD (n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当![]() 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)
【答案】(1)菱形,理由见解析;(2)![]() ;(3)6.
;(3)6.
【解析】试题分析:(1)根据矩形和线段垂直平分线的性质,由AAS证明ΔBOF≌ΔBOG,得到BG=GE=EF=FB,从而得出四边形BFEG是菱形的结论.
(2)根据矩形和菱形的性质,反复应用勾股定理即可求得FG的长.
(3)同(2)的思路,应用特殊元素法,列出关于n的方程求解即可.
试题解析:(1)(1)菱形,理由如下:
∵FG为BE的垂直平分线,∴FE=FB,GB=GE,∠FEB=∠FBO.
又∵FE∥BG,∴∠FEB=∠GBO. ∴∠FBO=∠GBO,BO=BO,∠BOF=∠BOG.
∴ΔBOF≌ΔBOG(AAS). ∴BF=BG.
∴BG=GE=EF=FB. ∴BFEG为菱形.
(2)∵AB=a,AD=2AB, ![]() ,∴AD=2a,
,∴AD=2a, ![]() .
.
∴根据勾股定理,得 BE=![]() . ∴OE=
. ∴OE=![]() .
.
设菱形BFEG的边长为x,
∵AB2+AF2=BF2,
∴![]() ,解得:x=
,解得:x=![]() .
.
∴OF=![]() .
.
∴FG=![]() .
.
(3)n=6.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目