题目内容
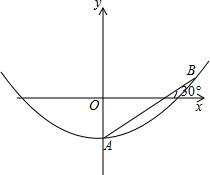
如图,现有一横截面是一抛物线的水渠.一次,水渠管理员将一根长1.5m的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,发现标杆有1m浸没在水中,露出水面部分的标杆与水面成30°的夹角(标杆与抛物线的横截面在同一平面内).(1)以水面所在直线为x轴,建立如图所示的直角坐标系,求该水渠横截面抛物线的解析式(结果保留根号);
(2)在(1)的条件下,求当水面再上升0.3m时的水面宽约为多少(
 取2.2,结果精确到0.1m).
取2.2,结果精确到0.1m).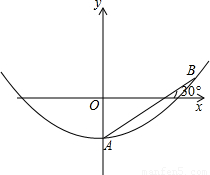
【答案】分析:(1)根据所建坐标系,设解析式为顶点式.因此需求顶点A的坐标和点B的坐标.设AB与x轴交于C点,可知AC=1m,BC=0.5m.作BD⊥x轴于点D.通过解Rt△AOC和Rt△BCD求点A、B的坐标.
(2)运用函数性质结合解方程求解.
解答: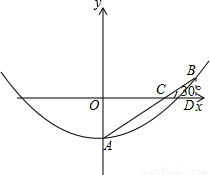 解:(1)设AB与x轴交于C点,可知AC=1m,BC=0.5m.
解:(1)设AB与x轴交于C点,可知AC=1m,BC=0.5m.
作BD⊥x轴于点D.
则OA=0.5m,OC=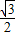 m,
m,
BD= m,CD=
m,CD=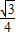 m,
m,
故A(0,- );
);
B(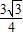 ,
, ).
).
设抛物线的解析式为y=ax2- .
.
将点B的坐标代入得a= ,
,
因而y= x2-
x2- .
.
(2)当水面上升0.3m时,
此时y=0.3,代入可得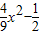 =0.3,
=0.3,
解得x=±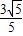 .
.
故此时水面宽为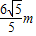 ,约为2.6m.
,约为2.6m.
点评:将实际问题转化为数学题体现了数学建模的思想,是解决实际问题的常用有效手段.如何建模需认真斟酌.
(2)运用函数性质结合解方程求解.
解答:
 解:(1)设AB与x轴交于C点,可知AC=1m,BC=0.5m.
解:(1)设AB与x轴交于C点,可知AC=1m,BC=0.5m.作BD⊥x轴于点D.
则OA=0.5m,OC=
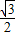 m,
m,BD=
 m,CD=
m,CD=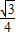 m,
m,故A(0,-
 );
);B(
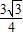 ,
, ).
).设抛物线的解析式为y=ax2-
 .
.将点B的坐标代入得a=
 ,
,因而y=
 x2-
x2- .
.(2)当水面上升0.3m时,
此时y=0.3,代入可得
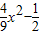 =0.3,
=0.3,解得x=±
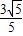 .
.故此时水面宽为
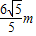 ,约为2.6m.
,约为2.6m.点评:将实际问题转化为数学题体现了数学建模的思想,是解决实际问题的常用有效手段.如何建模需认真斟酌.

练习册系列答案
相关题目
 面在同一平面内).
面在同一平面内). 取2.2,结果精确到0.1m).
取2.2,结果精确到0.1m).
 取2.2,结果精确到0.1m).
取2.2,结果精确到0.1m).
 取2.2,结果精确到0.1m).
取2.2,结果精确到0.1m).
 取2.2,结果精确到0.1m).
取2.2,结果精确到0.1m).