题目内容
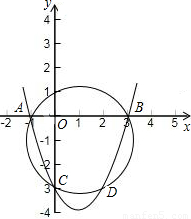
(1999•武汉)已知:如图,在直角坐标系中,直线AB交y轴于点A,交x轴于点B,其解析式为y=- x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.
x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.(1)求点C的纵坐标;
(2)以AO为直径作⊙O2,交直线AB于D,交⊙O1于N,连ON并延长交CD于G,求△ODG的面积;
(3)另有一圆过点O1,与y轴切于点O2,与直线AB交于M、P两点,求证:O1M•O1P=2.
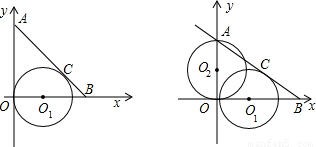
【答案】分析:(1)由解析式解出两点的坐标,过C点作CH垂直x轴,进而求纵横坐标.
(2)设直线AB与⊙O2的交点为D连接两点,求出CD,然后求出DG,从而求出面积.
(3)连接O1C,设⊙O1半径为r,由相似定理,进而证明.
解答:(1)解:由y=- x+2,得OA=2,OB=
x+2,得OA=2,OB=
∴AB=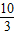 ,
,
由AC=2,得CB= ,
,
过C点作CH⊥x轴,垂足为H,得CH∥y轴,
则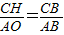 ,
,
CH= ,即点C的纵坐标为
,即点C的纵坐标为 .
.
(2)解:∵OA为⊙O2的直径,
∴OD⊥AB,
由OD•AB=OA•0B,得OD= ,
,
则AD=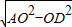 =
= ,
,
CD=2- =
= .
.
设DG=x,由切割线定理得GD•GA=GN•GO.
∴x(x+ )=(
)=( -x)2.解得:x=
-x)2.解得:x=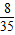 ,∴DG=
,∴DG=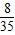 ,
,
∴S△ODG= OD•DG=
OD•DG=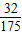 .
.
(3)证明:连接O1C,设⊙O1半径为r,
将C点纵坐标 代入y=-
代入y=- x+2,得x=
x+2,得x= ,
,
∴OH= ,O1H=
,O1H= -r.
-r.
在Rt△CHO1中,由勾股定理得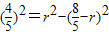 .
.
故⊙O1和⊙O2都是半径为1的等圆,
过点O1且与y轴切于点O2的圆是以N为圆心,1为半径的圆.
作⊙N的直径O1Q,连接PQ.O1Q=2,O1C=1.
∵∠PQO1=∠CMO1,
∴Rt△PQO1∽Rt△CMO1,
∴ ,
,
∴O1M•O1P=O1Q•O1C=2×1=2.
点评:本题主要考查一次函数的应用,本题比较烦,计算和证明都要仔细.
(2)设直线AB与⊙O2的交点为D连接两点,求出CD,然后求出DG,从而求出面积.
(3)连接O1C,设⊙O1半径为r,由相似定理,进而证明.
解答:(1)解:由y=-
 x+2,得OA=2,OB=
x+2,得OA=2,OB=
∴AB=
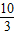 ,
,由AC=2,得CB=
 ,
,过C点作CH⊥x轴,垂足为H,得CH∥y轴,
则
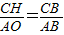 ,
,CH=
 ,即点C的纵坐标为
,即点C的纵坐标为 .
.(2)解:∵OA为⊙O2的直径,
∴OD⊥AB,
由OD•AB=OA•0B,得OD=
 ,
,则AD=
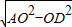 =
= ,
,CD=2-
 =
= .
.设DG=x,由切割线定理得GD•GA=GN•GO.
∴x(x+
 )=(
)=( -x)2.解得:x=
-x)2.解得:x=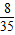 ,∴DG=
,∴DG=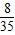 ,
,∴S△ODG=
 OD•DG=
OD•DG=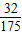 .
.(3)证明:连接O1C,设⊙O1半径为r,
将C点纵坐标
 代入y=-
代入y=- x+2,得x=
x+2,得x= ,
,∴OH=
 ,O1H=
,O1H= -r.
-r.在Rt△CHO1中,由勾股定理得
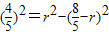 .
.故⊙O1和⊙O2都是半径为1的等圆,
过点O1且与y轴切于点O2的圆是以N为圆心,1为半径的圆.
作⊙N的直径O1Q,连接PQ.O1Q=2,O1C=1.
∵∠PQO1=∠CMO1,
∴Rt△PQO1∽Rt△CMO1,
∴
 ,
,∴O1M•O1P=O1Q•O1C=2×1=2.
点评:本题主要考查一次函数的应用,本题比较烦,计算和证明都要仔细.

练习册系列答案
相关题目
 (x-1)2+2,则这条抛物线的顶点坐标是 .
(x-1)2+2,则这条抛物线的顶点坐标是 . x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.
x+2.又O1是x轴上一点,且⊙O1与直线AB切于点C,与y轴切于原点O.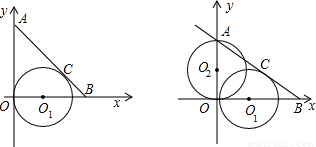
 (x-1)2+2,则这条抛物线的顶点坐标是 .
(x-1)2+2,则这条抛物线的顶点坐标是 .