题目内容
如图(1)所示,一个梯子AB长2.5米,顶端A靠在墙AC上(墙与地面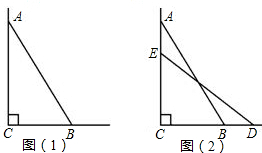 垂直),这时梯子下端B与墙角C距离为1.5米.
垂直),这时梯子下端B与墙角C距离为1.5米.(1)求梯子顶端A与地面的距离AC的长;
(2)若梯子滑动后停在DE位置上,如图(2)所示,测得BD=0.5米,求梯子顶端A下滑了多少米?
分析:(1)在Rt△ABC中,利用勾股定理求得AC;
(2)在Rt△ECD中,得到CD=CB+BD=1.5+0.5=2,然后由勾股定理求得CE,再由第一问求得的AC的长,求得AE的长即可.
(2)在Rt△ECD中,得到CD=CB+BD=1.5+0.5=2,然后由勾股定理求得CE,再由第一问求得的AC的长,求得AE的长即可.
解答:解:(1)在Rt△ABC中,∠C=90°
根据勾股定理,得:AC=
=
=2(米)
∴梯子顶端A与地面的距离AC为2米;
(2)依题意,得:CD=BC+BD=1.5+0.5=2(米)
在Rt△CDE中,∠C=90°,
根据勾股定理,得:CE=
=
=1.5(米)
∴AE=AC-CE=2-1.5=0.5(米)
∴梯子顶端A下滑了0.5米.
根据勾股定理,得:AC=
| AB2-BC2 |
=
| 2.52-1.52 |
=2(米)
∴梯子顶端A与地面的距离AC为2米;
(2)依题意,得:CD=BC+BD=1.5+0.5=2(米)
在Rt△CDE中,∠C=90°,
根据勾股定理,得:CE=
| DE2-CD2 |
| 2.52-22 |
∴AE=AC-CE=2-1.5=0.5(米)
∴梯子顶端A下滑了0.5米.
点评:本题考查了勾股定理的应用,将数学知识与生活中的实际问题相结合,是近几年中考的重点考点之一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
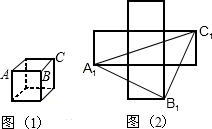 如图(1)所示是一个无盖的正方体纸盒,现将其展开成平面图,如图(2)所示,则∠B1A1C1与∠BAC的大小关系是
如图(1)所示是一个无盖的正方体纸盒,现将其展开成平面图,如图(2)所示,则∠B1A1C1与∠BAC的大小关系是
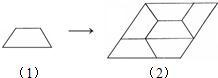 11、如图(1)是一个等腰梯形,由6个这样的等腰梯形恰好可以拼出如图(2)所示的一个菱形.对于图(1)中的等腰梯形,请写出它的内角的度数或腰与底边长度之间关系的一个正确结论:
11、如图(1)是一个等腰梯形,由6个这样的等腰梯形恰好可以拼出如图(2)所示的一个菱形.对于图(1)中的等腰梯形,请写出它的内角的度数或腰与底边长度之间关系的一个正确结论: