题目内容
 如图,点C为AB 弧的中点,点D为⊙O上一点,∠D=30°,BC=4cm,求⊙O的半径长.
如图,点C为AB 弧的中点,点D为⊙O上一点,∠D=30°,BC=4cm,求⊙O的半径长.
 解:如图,作直径AE,连接CE、AC,
解:如图,作直径AE,连接CE、AC,∵C为弧AB的中点,
∴弧AC=弧BC,
∴AC=BC=4cm,
∵AE是圆O的直径,
∴∠ACE=90°,
∵弧AC=弧AC,
∴∠E=∠D=30°,
∴AD=2AC=8cm,
∴⊙O的半径是4cm.
答:⊙O的半径是4cm.
分析:作直径AE,连接CE、AC,根据圆周角定理求出∠ACE=90°,∠E=∠D,根据圆心角、弧、弦之间的关系求出AC的长,根据含30度角的直角三角形性质求出直径即可.
点评:本题考查了对圆周角定理,圆心角、弧、弦之间的关系,含30度角的直角三角形性质等知识点的理解和运用,正确作辅助线后求出AC和∠ACE、∠E是解此题的关键所在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,⊙O的直径AB长为2,弧AC的度数为100°,弧BD的度数为40°,点P是直径AB上的动点,则PC+PD的最小值是
如图,⊙O的直径AB长为2,弧AC的度数为100°,弧BD的度数为40°,点P是直径AB上的动点,则PC+PD的最小值是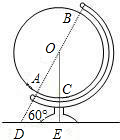 如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为60°,半径OC所在的直线与放置平面垂直,垂足为点E,DE=15cm,AD=14cm.
如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为60°,半径OC所在的直线与放置平面垂直,垂足为点E,DE=15cm,AD=14cm. (2011•海安县模拟)如图,点C为AB 弧的中点,点D为⊙O上一点,∠D=30°,BC=4cm,求⊙O的半径长.
(2011•海安县模拟)如图,点C为AB 弧的中点,点D为⊙O上一点,∠D=30°,BC=4cm,求⊙O的半径长.