题目内容
请先阅读下列一段内容,然后解答后面问题:
=1-
,
=
-
,
=
-
,…
①第四个等式为
=
-
=
-
,第n个等式为
=
-
=
-
;
②根据你发现的规律计算:
+
+
+…+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
①第四个等式为
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
②根据你发现的规律计算:
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 11×12 |
分析:①先根据所给的式子找出第一、第二、第三个式子的规律,进而可求出第四、第n个式子的表达式;
②把所给式子相加,找出规律即可进行计算.
②把所给式子相加,找出规律即可进行计算.
解答:解:①∵第一个式子为:
=1-
,
第二个式子为:
=
-
,
第三个式子为:
=
-
,
∴第四个等式为:
=
-
,第n个等式为:
=
-
.
故答案为:
=
-
,
=
-
;
②∵第一、第二、第三个式子相加=1-
+
-
+
-
=1-
,
∴
+
+
+…+
=1-
+
-
+
-
+…
-
=1-
=
.
| 1 |
| 1×2 |
| 1 |
| 2 |
第二个式子为:
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
第三个式子为:
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
∴第四个等式为:
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
故答案为:
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
②∵第一、第二、第三个式子相加=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
∴
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 11×12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 11 |
| 1 |
| 12 |
| 1 |
| 12 |
| 11 |
| 12 |
点评:本题考查的是有理数的混合运算,是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题,熟练掌握分数的拆分计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =1-
=1- ,
, =
= ,
, =
= ,…
,…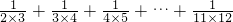 .
. ,
, ,
, ,…,
,…,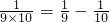 ,
,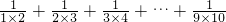 =
=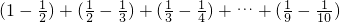 =
=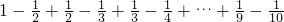 =
=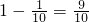 .
.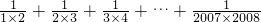 ;
; .
.