题目内容
 一水池内有水90立方米,设全池水排尽的时间为y分钟,每分钟的排水量为x立方米,
一水池内有水90立方米,设全池水排尽的时间为y分钟,每分钟的排水量为x立方米,
排水时间的范围是9≤y≤15
(1)求y关于x的函数解析式,并指出每分钟排水量x的取值范围;
(2)在坐标系中画出此函数的图象;
(3)根据图象求当每分钟排水量为9立方米时,排水需多少分钟?当排水时间为10分钟时,每分钟的排水量是多少立方米?
解:(1)∵每小时排水量×排水时间=蓄水池的容积,
∴y=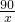 ,
,
∵排水时间的范围是9≤y≤15
∴6≤x≤10;
(2)
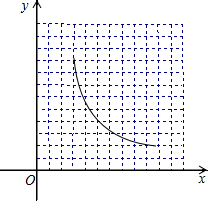
(3)令x=9,解得y=10,
令y=10求得x=9,
∴当每分钟排水量为9立方米时,排水需10分钟;当排水时间为10分钟时,每分钟的排水量是9立方米.
分析:(1)根据:每小时排水量×排水时间=蓄水池的容积,可以得到函数关系式;
(2)根据自变量的取值范围作出函数的图象即可;
(3)分别将x=9和y=10代入解析式求解即可;
点评:本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式,再运用函数关系式解题.
∴y=
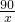 ,
,∵排水时间的范围是9≤y≤15
∴6≤x≤10;
(2)

(3)令x=9,解得y=10,
令y=10求得x=9,
∴当每分钟排水量为9立方米时,排水需10分钟;当排水时间为10分钟时,每分钟的排水量是9立方米.
分析:(1)根据:每小时排水量×排水时间=蓄水池的容积,可以得到函数关系式;
(2)根据自变量的取值范围作出函数的图象即可;
(3)分别将x=9和y=10代入解析式求解即可;
点评:本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式,再运用函数关系式解题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 一水池内有水90立方米,设全池水排尽的时间为y分钟,每分钟的排水量为x立方米,
一水池内有水90立方米,设全池水排尽的时间为y分钟,每分钟的排水量为x立方米,