题目内容
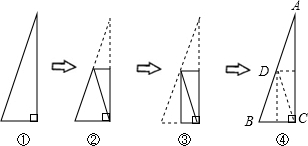
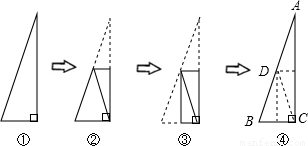
在折纸游戏中，把一三角形ABC纸片一角∠C沿EF折叠（EF∥AB），使顶点C落在四边形ABEF的中位线上，如图2所示，请猜测EF：AB=________．
1：3
分析：设四边形ABEF的中位线为GH，根据梯形中位线定理得GH为四边形ABEF的中位线，由三角形中位线定理可得EF为△CGH的中位线，从而不难求得EF：AB的值．
解答：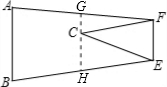
解：设四边形ABEF的中位线为GH
∵四边形ABEF为梯形，EF为△CGH的中位线
∴GH=2EF
∵GH是四边形ABEF的中位线
∴GH=
（AB+EF）
∴2EF=（AB+EF）
∴EF：AB=1：3
点评：此题主要考查梯形的中位线定理和三角形的中位线定理．
分析：设四边形ABEF的中位线为GH，根据梯形中位线定理得GH为四边形ABEF的中位线，由三角形中位线定理可得EF为△CGH的中位线，从而不难求得EF：AB的值．
解答：
解：设四边形ABEF的中位线为GH∵四边形ABEF为梯形，EF为△CGH的中位线
∴GH=2EF
∵GH是四边形ABEF的中位线
∴GH=
（AB+EF）∴2EF=
（AB+EF）∴EF：AB=1：3
点评：此题主要考查梯形的中位线定理和三角形的中位线定理．
练习册系列答案
相关题目
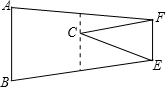在折纸游戏中，把一三角形ABC纸片一角∠C沿EF折叠（EF∥AB），使顶点C落在四边形ABEF的中位线上，如图2所示，请猜测EF：AB=
