题目内容
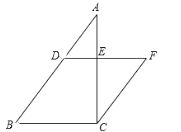
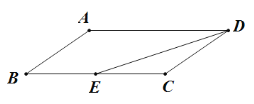
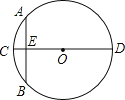
【题目】如图,已知四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
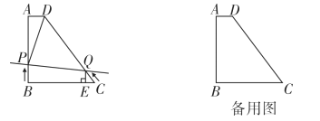
(1)求四边形![]() 的面积
的面积![]() ;
;
(2)动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿
出发,以每秒1个单位长度的速度,沿![]() 方向,向点
方向,向点![]() 运动;动点
运动;动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度,沿
出发,以每秒1个单位长度的速度,沿![]() 方向,向点
方向,向点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() .若
.若![]() 、
、![]() 两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为
两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为![]() .问:
.问:
①当点![]() 在
在![]() 上运动时,是否存在这样的
上运动时,是否存在这样的![]() ,使得直线
,使得直线![]() 将四边形
将四边形![]() 的周长平分?若存在,请求出
的周长平分?若存在,请求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②在运动过程中,是否存在这样的![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出所有符合条件的
相似?若存在,请求出所有符合条件的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)40;(2)①当![]() 时,
时,![]() 将四边形
将四边形![]() 的周长平分.②
的周长平分.②![]() 或
或![]() 时,以
时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
【解析】
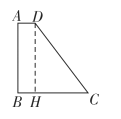
(1)作![]() 交
交![]() 于点
于点![]() ,利用勾股定理的逆定理证得四边形
,利用勾股定理的逆定理证得四边形![]() 是直角梯形,然后根据直角梯形的面积公式即可求得;
是直角梯形,然后根据直角梯形的面积公式即可求得;
(2)①利用周长平分,列出方程即可求解;
②当点P在AB上时,分![]() 和
和![]() 两种情况,根据等角的正切函数构建方程即可求解;当点P在AD和DC上时,不可能构成与
两种情况,根据等角的正切函数构建方程即可求解;当点P在AD和DC上时,不可能构成与![]() 相似的三角形.
相似的三角形.
(1)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() ;
;![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
∴四边形![]() 是直角梯形.
是直角梯形.
![]() .
.
(2)①当点![]() 在
在![]() 上运动时,
上运动时,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴当![]() 时,
时,![]() 将四边形
将四边形![]() 的周长平分.
的周长平分.
②∵![]() ,
,![]() ,
,![]() ,
,
∴点![]() 运动到
运动到![]() 时运动停止,
时运动停止,
∴![]() .
.
第一种情况:![]() ,若
,若![]() ,则
,则![]() .
.
∴![]() .
.
∴![]() ,∴
,∴![]() .
.
若![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
第二种情况:![]() ,
,![]() 、
、![]() 、
、![]() 三点不能组成三角形;
三点不能组成三角形;
第三种情况:![]() ,
,![]() 为钝角三角形与
为钝角三角形与![]() 不相似;
不相似;
∴![]() 或
或![]() 时,以
时,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.

【题目】如图,某商场设立了一个可以自由转动的转盘,并规定:顾客购物50元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在某一区域就可以获得该区域相对应的奖品.若恰巧落在两区域交界线上,则重新转动转盘.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“矿泉水”的次数 | 68 | 111 | 136 | 345 | 564 | 701 |
假如你去转动该转盘一次,你获得牙膏的概率约是______.(用小数表示,结果保留一位小数)