题目内容
 如图,在边长为2的圆内接正方形ABCD中,AC是对角线,P为边CD的中点,延长AP交圆于点E.
如图,在边长为2的圆内接正方形ABCD中,AC是对角线,P为边CD的中点,延长AP交圆于点E.
(1)∠E=______度;
(2)写出图中现有的一对不全等的相似三角形,并说明理由;
(3)求弦DE的长.
 解:(1)∵∠ACD=45°,∠ACD=∠E,
解:(1)∵∠ACD=45°,∠ACD=∠E,∴∠E=45°.
(2)△ACP∽△DEP,
理由:∵∠AED=∠ACD,∠APC=∠DPE,
∴△ACP∽△DEP.
(3)方法一:
∵△ACP∽△DEP,
∴
 .
.∵P为CD边中点,
∴DP=CP=1
∵AP=
 ,AC=
,AC= ,
,∴DE=
 .
.方法二:
如图2,过点D作DF⊥AE于点F,
在Rt△ADP中,AP=
 .
.又∵S△ADP=
 AD•DP=
AD•DP= AP•DF,
AP•DF,∴DF=
 .
.∴DE=
 DF=
DF= .
.分析:由“同弧所对的圆周角相等”可知∠E=∠ACD=45°,∠CAE=∠EDC,所以△ACP∽△DEP;求弦DE的长有两种方法:
一,利用△ACP∽△DEP的相似比
 求DE的长;
求DE的长;二、过点D作DF⊥AE于点F,利用Rt△DFE中的勾股定理求得DE的长.
点评:此题主要考查相似三角形的判定及圆周角定理的运用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
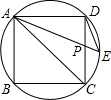 如图,在边长为2的圆内接正方形ABCD中,AC是对角线,P为边CD的中点,延长AP交圆于点E.
如图,在边长为2的圆内接正方形ABCD中,AC是对角线,P为边CD的中点,延长AP交圆于点E.


