题目内容
如下图直线![]() 分别与x轴、y轴交于点A、B,⊙E经过原点O及A、B两点.
分别与x轴、y轴交于点A、B,⊙E经过原点O及A、B两点.
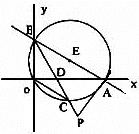
(1)C是⊙E上一点,连结BC交OA于点D,若∠COD=∠CBO,求点A、B、C的坐标;
(2)求经过O、C、A三点的抛物线的解析式:
(3)若延长BC到P,使DP=2,连结AP,试判断直线PA与⊙E的位置关系,并说明理由.
答案:
解析:
解析:
|
(1)连结EC交x轴于点N(如图).
∵A、B是直线 又∠COD=∠CBO.∴∠CBO=∠ABC.∴C是 ∴ 连结OE.∴ (2)设经过O、C、A三点的抛物线的解析式为 ∵C( ∴ (3)∵ 由(1)知∠OBD=∠ABD.∴ ∴OD=OB·tan30°=1.∴DA=2. ∵∠ADC=∠BDO=60°,PD=AD=2.∴△ADP是等边三角形. ∴∠DAP=60°. ∴∠BAP=∠BAO+∠DAP=30°+60°=90°.即PA⊥AB. 即直线PA是⊙E的切线. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



 轴的负方向平移6个单位,它与点_______________重合。
轴的负方向平移6个单位,它与点_______________重合。 轴的距离是多少?
轴的距离是多少?
 轴的负方向平移6个单位,它与点_______________重合。
轴的负方向平移6个单位,它与点_______________重合。 轴的距离是多少?
轴的距离是多少?

