题目内容
一条直线y=kx+b与两坐标轴所围成的三角形的面积为18.
(1)当这条直线与直线y=x+1平行时,求其解析式;
(2)若这条直线在y轴上截距为6时,求其解析式.
(1)当这条直线与直线y=x+1平行时,求其解析式;
(2)若这条直线在y轴上截距为6时,求其解析式.
考点:两条直线相交或平行问题,一次函数图象上点的坐标特征
专题:
分析:(1)根据平行直线的解析式的k值相等可得k=1,然后求出直线与坐标轴的交点,再利用三角形的面积公式列式计算即可得解;
(2)设直线与x轴的交点到原点的距离为a,然后利用三角形的面积求出a,再分两种情况写出与x轴的交点坐标,然后代入直线解析式计算即可得解.
(2)设直线与x轴的交点到原点的距离为a,然后利用三角形的面积求出a,再分两种情况写出与x轴的交点坐标,然后代入直线解析式计算即可得解.
解答:解:(1)∵直线y=kx+b与直线y=x+1平行,
∴k=1,
∴y=x+b,
令x=0,则y=b,
令y=0,则x+b=b,解得x=-b,
∴三角形的面积=
b2=18,
解得b=±6,
∴直线解析式为y=x+6或y=x-6;
(2)设直线与x轴的交点到原点的距离为a,
则三角形的面积=
a×6=18,
解得a=6,
∴直线与x轴的交点坐标为(6,0)或(-6,0),
∵直线在y轴上截距为6,
∴直线解析式为y=kx+6,
把(6,0)代入得,k=-1,
把(-6,0)代入得,k=1,
∴直线解析式为y=-x+6或y=x+6.
∴k=1,
∴y=x+b,
令x=0,则y=b,
令y=0,则x+b=b,解得x=-b,
∴三角形的面积=
| 1 |
| 2 |
解得b=±6,
∴直线解析式为y=x+6或y=x-6;
(2)设直线与x轴的交点到原点的距离为a,
则三角形的面积=
| 1 |
| 2 |
解得a=6,
∴直线与x轴的交点坐标为(6,0)或(-6,0),
∵直线在y轴上截距为6,
∴直线解析式为y=kx+6,
把(6,0)代入得,k=-1,
把(-6,0)代入得,k=1,
∴直线解析式为y=-x+6或y=x+6.
点评:本题考查了两直线相交或平行问题,一次函数图象上点的坐标特征,(1)熟记平行直线的解析式的k值相等是解题的关键,(2)要注意求出直线与x轴交点坐标后分情况讨论.

练习册系列答案
相关题目
 如图,矩形ABCD中,O是对角线AC、BD的交点,△ABO与△ADO的周长的差为2cm,和为34cm,两对角线长的和为20cm,求矩形的周长和面积.
如图,矩形ABCD中,O是对角线AC、BD的交点,△ABO与△ADO的周长的差为2cm,和为34cm,两对角线长的和为20cm,求矩形的周长和面积. 如图,∠B=∠C=∠EDF,若△DEF与△BDF、△CED都相似,请写出你能够得到的结论,并请说明理由.
如图,∠B=∠C=∠EDF,若△DEF与△BDF、△CED都相似,请写出你能够得到的结论,并请说明理由.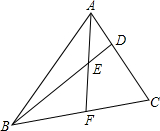 如图,在△ABC中,D、F分别是AC、BC上的点,且AD:DC=1:2,点F是BC边的中点,AF、BD相交于点E,求证:BE:ED=3:1.
如图,在△ABC中,D、F分别是AC、BC上的点,且AD:DC=1:2,点F是BC边的中点,AF、BD相交于点E,求证:BE:ED=3:1.