题目内容
【题目】已知抛物线![]() (m为常数,﹣1≤m≤4).A(﹣m﹣1,
(m为常数,﹣1≤m≤4).A(﹣m﹣1,![]() ),B(
),B(![]() ,
,![]() ),C(﹣m,
),C(﹣m,![]() )是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较![]() ,
,![]() ,
,![]() 之间的大小.
之间的大小.
【答案】(1)顶点坐标(![]() ,
,![]() );(2)k=3;(3)﹣1≤m<
);(2)k=3;(3)﹣1≤m<![]() 或
或![]() <m≤
<m≤![]() 时,有
时,有![]() ,
,![]() <m<
<m<![]() 时,有
时,有![]() .
.
【解析】
试题分析:(1)根据顶点坐标公式即可解决问题.
(2)列方程组根据△=0解决问题.
(3)首先证明![]() ,再根据点B的位置,分类讨论,①令
,再根据点B的位置,分类讨论,①令![]() <﹣m﹣1,求出m的范围即可判断,②令
<﹣m﹣1,求出m的范围即可判断,②令![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令![]() >﹣m﹣1,求出m的范围即可判断,④令
>﹣m﹣1,求出m的范围即可判断,④令![]() ≤
≤![]() <﹣m,求出m的范围即可判断,⑤令
<﹣m,求出m的范围即可判断,⑤令![]() =﹣m,B,C重合,不合题意舍弃.⑥令
=﹣m,B,C重合,不合题意舍弃.⑥令![]() >﹣m,求出m的范围即可判断.
>﹣m,求出m的范围即可判断.
试题解析:(1)∵![]() =
=![]() ,
,![]() =
=![]() ,∴顶点坐标(
,∴顶点坐标(![]() ,
,![]() ).
).
(2)由 ,消去y得
,消去y得![]() ,∵抛物线与x轴有且仅有一个公共点,∴△=0,即(k﹣3)m=0,∵无论m取何值,方程总是成立,∴k﹣3=0,∴k=3;
,∵抛物线与x轴有且仅有一个公共点,∴△=0,即(k﹣3)m=0,∵无论m取何值,方程总是成立,∴k﹣3=0,∴k=3;
(3)PH=![]() =
=![]() ,∵1<PH≤6,∴当
,∵1<PH≤6,∴当![]() >0时,有1<
>0时,有1<![]() ≤6,又﹣1≤m≤4,∴
≤6,又﹣1≤m≤4,∴![]() <m≤
<m≤![]() ,当
,当![]() <0时,1<
<0时,1<![]() ≤6,又∵﹣1≤m≤4,∴﹣1≤m≤
≤6,又∵﹣1≤m≤4,∴﹣1≤m≤![]() ,∴﹣1≤m<
,∴﹣1≤m<![]() 或
或![]() <m≤
<m≤![]() ,∵A(﹣m﹣1,
,∵A(﹣m﹣1,![]() )在抛物线上,∴
)在抛物线上,∴![]() =﹣4m,∵C(﹣m,
=﹣4m,∵C(﹣m,![]() )在抛物线上,∴
)在抛物线上,∴![]() =﹣4m,∴
=﹣4m,∴![]() ;
;
①令![]() <﹣m﹣1,则有m<
<﹣m﹣1,则有m<![]() ,结合﹣1≤m≤
,结合﹣1≤m≤![]() ,∴﹣1≤m<
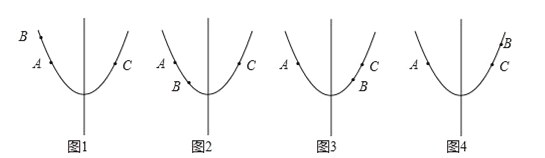
,∴﹣1≤m<![]() ,此时,在对称轴的左侧y随x的增大而减小,如图1,∴
,此时,在对称轴的左侧y随x的增大而减小,如图1,∴![]() ,即当﹣1≤m<
,即当﹣1≤m<![]() 时,有
时,有![]() .
.
②令![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令![]() >﹣m﹣1,且
>﹣m﹣1,且![]() ≤
≤![]() 时,有
时,有![]() <m≤
<m≤![]() ,结合﹣1≤m<
,结合﹣1≤m<![]() ,∴
,∴![]() <m≤
<m≤![]() ,此时,在对称轴的左侧,y随x的增大而减小,如图2,∴
,此时,在对称轴的左侧,y随x的增大而减小,如图2,∴![]() ,即当
,即当![]() <m≤
<m≤![]() 时,有
时,有![]() ;
;
④令![]() ≤
≤![]() <﹣m,有
<﹣m,有![]() ≤m<0,结合﹣1≤m<
≤m<0,结合﹣1≤m<![]() ,∴
,∴![]() ≤m<
≤m<![]() ,此时,在对称轴的右侧y随x的增大而增大,如图3,∴
,此时,在对称轴的右侧y随x的增大而增大,如图3,∴![]() .
.
⑤令![]() =﹣m,B,C重合,不合题意舍弃.
=﹣m,B,C重合,不合题意舍弃.
⑥令![]() >﹣m,有m>0,结合
>﹣m,有m>0,结合![]() <m≤
<m≤![]() ,∴
,∴![]() <m≤
<m≤![]() ,此时,在对称轴的右侧,y随x的增大而增大,如图4,∴
,此时,在对称轴的右侧,y随x的增大而增大,如图4,∴![]() ,即当
,即当![]() <m≤
<m≤![]() 时,有
时,有![]() ;
;
综上所述,﹣1≤m<![]() 或
或![]() <m≤
<m≤![]() 时,有
时,有![]() ,
,![]() <m<
<m<![]() 时,有
时,有![]() .
.