题目内容
【题目】阅读材料:
在一个三角形中,各边和它所对角的正弦的比相等, ![]() =
= ![]() =
= ![]() ,利用上述结论可以求解如下题目:
,利用上述结论可以求解如下题目:
在△ABC中,∠A、∠B、∠C的对边分别为a,b,c.若∠A=45°,∠B=30°,a=6,求b.
解:在△ABC中,∵ ![]() =
= ![]() ∴b=
∴b= ![]() =
= ![]() =
= ![]() =3
=3 ![]() .
.
理解应用:
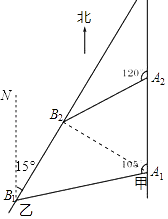
如图,甲船以每小时30 ![]() 海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,且乙船从B1处按北偏东15°方向匀速直线航行,当甲船航行20分钟到达A2时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 ![]() 海里.
海里.
(1)判断△A1A2B2的形状,并给出证明;
(2)求乙船每小时航行多少海里?
【答案】
(1)
解:△A1A2B2是等边三角形,理由如下:
连结A1B2.
∵甲船以每小时30 ![]() 海里的速度向正北方向航行,航行20分钟到达A2,
海里的速度向正北方向航行,航行20分钟到达A2,
∴A1A2=30 ![]() ×
× ![]() =10
=10 ![]() ,
,
又∵A2B2=10 ![]() ,∠A1A2B2=60°,
,∠A1A2B2=60°,
∴△A1A2B2是等边三角形;
(2)
解:过点B作B1N∥A1A2,如图,
∵B1N∥A1A2,
∴∠A1B1N=180°﹣∠B1A1A2=180°﹣105°=75°,
∴∠A1B1B2=75°﹣15°=60°.
∵△A1A2B2是等边三角形,
∴∠A2A1B2=60°,A1B2=A1A2=10 ![]() ,
,
∴∠B1A1B2=105°﹣60°=45°.
在△B1A1B2中,
∵A1B2=10 ![]() ,∠B1A1B2=45°,∠A1B1B2=60°,
,∠B1A1B2=45°,∠A1B1B2=60°,
由阅读材料可知, ![]() =
= ![]() ,
,
解得B1B2= 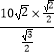 =
= ![]() ,
,
所以乙船每小时航行: ![]() ÷
÷ ![]() =20
=20 ![]() 海里.
海里.
【解析】(1)先根据路程=速度×时间求出A1A2=30 ![]() ×
× ![]() =10
=10 ![]() ,又A2B2=10
,又A2B2=10 ![]() ,∠A1A2B2=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出△A1A2B2是等边三角形;(2)先由平行线的性质及方向角的定义求出∠A1B1B2=75°﹣15°=60°,由等边三角形的性质得出∠A2A1B2=60°,A1B2=A1A2=10
,∠A1A2B2=60°,根据有一个角是60°的等腰三角形是等边三角形即可得出△A1A2B2是等边三角形;(2)先由平行线的性质及方向角的定义求出∠A1B1B2=75°﹣15°=60°,由等边三角形的性质得出∠A2A1B2=60°,A1B2=A1A2=10 ![]() ,那么∠B1A1B2=105°﹣60°=45°.然后在△B1A1B2中,根据阅读材料可知,
,那么∠B1A1B2=105°﹣60°=45°.然后在△B1A1B2中,根据阅读材料可知, ![]() =
= ![]() ,求出B1B2的距离,再由时间求出乙船航行的速度.
,求出B1B2的距离,再由时间求出乙船航行的速度.

 名校课堂系列答案
名校课堂系列答案【题目】某化妆品专卖店,为了吸引顾客,在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满88元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如表)
甲种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 6 | 12 | 6 |
乙种品牌化妆品 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 12 | 6 | 12 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满88元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.





