题目内容
已知α,β为锐角,tanα,tanβ是一元二次方程6x2-5x+1=0的两根,求锐角α+β的值.(备选公式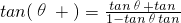 )
)
解:∵tanα,tanβ是一元二次方程6x2-5x+1=0的两根,
∴tanα+tanβ= ,tanα•tanβ=
,tanα•tanβ=
∵tan(α+β)=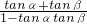 ,
,
∴tan(α+β)= =1,
=1,
∴锐角(α+β)=45°.
分析:根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系得到tanα+tanβ= ,tanα•tanβ=
,tanα•tanβ= ,然后利用题中给的公式有tan(α+β)=
,然后利用题中给的公式有tan(α+β)=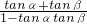 ,把
,把
tanα+tanβ= ,tanα•tanβ=
,tanα•tanβ= 整体代入得到tan(α+β)=
整体代入得到tan(α+β)= =1,再根据特殊角的三角函数值即可得到锐角α+β的值.
=1,再根据特殊角的三角函数值即可得到锐角α+β的值.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:如果方程的两根为x1,x2,则x1+x2=- ,x1•x2=
,x1•x2= .也考查了整体的思想以及特殊角的三角函数值.
.也考查了整体的思想以及特殊角的三角函数值.
∴tanα+tanβ=
 ,tanα•tanβ=
,tanα•tanβ=
∵tan(α+β)=
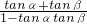 ,
,∴tan(α+β)=
 =1,
=1,∴锐角(α+β)=45°.
分析:根据一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系得到tanα+tanβ=
 ,tanα•tanβ=
,tanα•tanβ= ,然后利用题中给的公式有tan(α+β)=
,然后利用题中给的公式有tan(α+β)=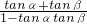 ,把
,把tanα+tanβ=
 ,tanα•tanβ=
,tanα•tanβ= 整体代入得到tan(α+β)=
整体代入得到tan(α+β)= =1,再根据特殊角的三角函数值即可得到锐角α+β的值.
=1,再根据特殊角的三角函数值即可得到锐角α+β的值.点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:如果方程的两根为x1,x2,则x1+x2=-
 ,x1•x2=
,x1•x2= .也考查了整体的思想以及特殊角的三角函数值.
.也考查了整体的思想以及特殊角的三角函数值. 
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知sinα=
,α为锐角,则tanα的值为( )
| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
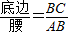 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C. D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.
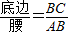 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C.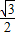 D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.
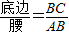 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C.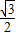 D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.
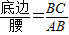 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的. B.1 C.
B.1 C.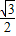 D.2
D.2 ,其中α为锐角,试求sadα的值.
,其中α为锐角,试求sadα的值.