题目内容
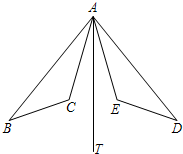 如图,已知:∠BAD与∠CAE的平分线都是AT,AC=AE,∠B=∠D.
如图,已知:∠BAD与∠CAE的平分线都是AT,AC=AE,∠B=∠D.求证:△ABC≌△ADE.
分析:由∠BAD与∠CAE的平分线都是AT,根据角平分线的性质,即可证得∠BAC=∠DAE,然后由AC=AE,∠B=∠D,根据AAS,即可证得:△ABC≌△ADE.
解答:解:∵∠BAD与∠CAE的平分线都是AT,
∴∠BAT=∠DAT,∠CAT=∠EAT,
∴∠BAT-∠CAT=∠DAT-∠EAT,
即∠BAC=∠DAE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS).
∴∠BAT=∠DAT,∠CAT=∠EAT,
∴∠BAT-∠CAT=∠DAT-∠EAT,
即∠BAC=∠DAE,
在△ABC和△ADE中,
|
∴△ABC≌△ADE(AAS).
点评:此题考查了全等三角形的判定与性质、角平分线的定义.此题难度不大,解题的关键是掌握判定两个三角形全等的一般方法(SSS、SAS、ASA、AAS、HL).注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 1、如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点.如果AB=6cm,BD=7cm,AD=4cm,那么BC的长为( )
1、如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点.如果AB=6cm,BD=7cm,AD=4cm,那么BC的长为( )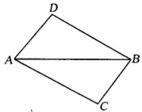 17、如图,已知△ABC≌△BAD,A和B、C和D是对应顶点.如果AB=6,BD=5,AD=4,那么BC的长度是
17、如图,已知△ABC≌△BAD,A和B、C和D是对应顶点.如果AB=6,BD=5,AD=4,那么BC的长度是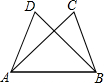 如图,已知△ABC≌△BAD,AB=6cm,BD=7cm,AD=5cm,则BC的长等于( )
如图,已知△ABC≌△BAD,AB=6cm,BD=7cm,AD=5cm,则BC的长等于( ) 如图,已知,∠BAD=120°,AC平分∠BAD,若∠ABC+∠ADC=180°,则如下结论一定正确的有( )个
如图,已知,∠BAD=120°,AC平分∠BAD,若∠ABC+∠ADC=180°,则如下结论一定正确的有( )个