题目内容
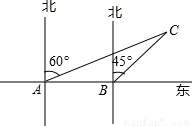
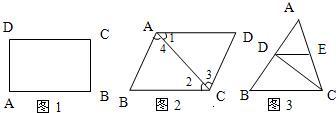
13、(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为
(2)如图2,若∠
(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=
2
cm;(2)如图2,若∠
1
=∠2
,则AD∥BC;(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=
25
度;
分析:(1)夹在两条平行线间的垂线段的长度即为两平行线的距离.
(2)运用的是平行线判定定理.
(3)运用的是角平分线的定义和平行线的性质.
(2)运用的是平行线判定定理.
(3)运用的是角平分线的定义和平行线的性质.
解答:解:(1)已知四边形ABCD为长方形,则AB∥CD,∠C=90°,∠B=90°.
又BC=2cm,故AB与CD之间的距离为2cm.
故填2.
(2)要使AD∥BC,根据平行线的判定定理可得∠1=∠2.
故填∠1;∠2.
(3)已知DE∥BC,
根据平行线判定定理可得∠EDC=∠DCB,
又CD是∠ACB的平分线,
∴∠ECD=∠DCB,
∵∠ACB=50°,
∴∠EDC=25°.
故填25.
又BC=2cm,故AB与CD之间的距离为2cm.
故填2.
(2)要使AD∥BC,根据平行线的判定定理可得∠1=∠2.
故填∠1;∠2.
(3)已知DE∥BC,
根据平行线判定定理可得∠EDC=∠DCB,
又CD是∠ACB的平分线,
∴∠ECD=∠DCB,
∵∠ACB=50°,
∴∠EDC=25°.
故填25.
点评:此类题考查的是平行线的性质以及平行线的判定定理,考生一定要熟记.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
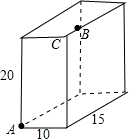 如图,长方体的长为15cm,宽为10cm,高为20cm,点B在棱CD上,CB=5cm.一只壁虎要沿长方休的表面从A点爬到B点,需要爬行的最短路径是多少cm?
如图,长方体的长为15cm,宽为10cm,高为20cm,点B在棱CD上,CB=5cm.一只壁虎要沿长方休的表面从A点爬到B点,需要爬行的最短路径是多少cm?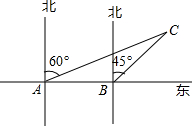 圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?(
圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险?(
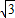 ≈1.73)
≈1.73)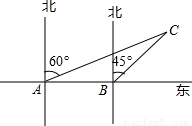
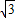 ≈1.73)
≈1.73)