题目内容
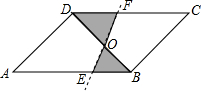 如图,在面积为8的平行四边形ABCD中,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交AB、CD于点E、F,若AE=2EB,则图中阴影部分的面积等于( )
如图,在面积为8的平行四边形ABCD中,对角线BD绕着它的中点O按顺时针方向旋转一定角度后,其所在直线分别交AB、CD于点E、F,若AE=2EB,则图中阴影部分的面积等于( )分析:过点D作DH⊥AB,交AB于点H,S?ABCD=AB•DH,S阴影部分=
DF•DH,继而即可求出答案.
| 1 |
| 2 |
解答:解:过点D作DH⊥AB,交AB于点H,如下图所示,

则S?ABCD=AB•DH=8,
又S阴影部分=
DF•DH,
∵AE=2EB,
根据旋转的性质可知,DF=EB,
∴S阴影部分=
×
S阴影部分=
.
故选C.

则S?ABCD=AB•DH=8,
又S阴影部分=
| 1 |
| 2 |
∵AE=2EB,
根据旋转的性质可知,DF=EB,
∴S阴影部分=
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
故选C.
点评:本题考查平行四边形及旋转的性质,解题关键是熟练掌握平行四边形及三角形的面积公式,难度一般.

练习册系列答案
相关题目
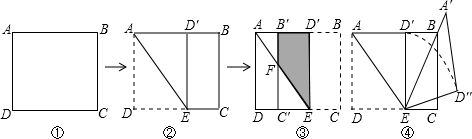
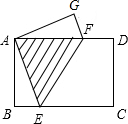 如图,在矩形纸片ABCD中,已知AB=3cm,BC=4cm,现将纸片折叠压平,使A,C重合,折痕为EF,试求重叠部分△AEF的面积.
如图,在矩形纸片ABCD中,已知AB=3cm,BC=4cm,现将纸片折叠压平,使A,C重合,折痕为EF,试求重叠部分△AEF的面积.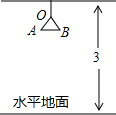 (2012•龙湾区二模)如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为( )
(2012•龙湾区二模)如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为( ) 如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为
如图,在某圆锥形灯罩的轴截面中,OA=OB,∠AOB=60°,已知一平顶房间高度为3米,若此灯罩的光源O发出的光线到达该房间水平地面的最大圆面面积为2.25π平方米(假设该水平地面足够大),则点O到此房间顶端的距离约为