题目内容
【题目】问题探究:(1)如图①,AB为⊙O的弦,点C是⊙O上的一点,在直线AB上方找一个点D,使得∠ADB=∠ACB,画出∠ADB;
(2)如图②,AB 是⊙O的弦,点C是⊙O上的一个点,在过点C的直线l上找一点P,使得∠APB<∠ACB,画出∠APB;
(3)如图③,已知足球门宽AB约为![]() 米,一球员从距B点
米,一球员从距B点![]() 米的C点(点A、B、C均在球场的底线上),沿与AC成45°的CD方向带球.试问,该球员能否在射线CD上找一点P,使得点P最佳射门点(即∠APB最大)?若能找到,求出这时点P与点C的距离;若找不到,请说明理由.
米的C点(点A、B、C均在球场的底线上),沿与AC成45°的CD方向带球.试问,该球员能否在射线CD上找一点P,使得点P最佳射门点(即∠APB最大)?若能找到,求出这时点P与点C的距离;若找不到,请说明理由.

【答案】(1)画图见解析;
(2)画图见解析;
(3)能找到点P,点P与点C的距离为10.
【解析】(本题满分10分)
解:(1)略-------------------------------------------------------1分
(2)略------------------------------------------------------3分
(3)能找到点P.如图,过AB两点的⊙O与射线CD相切于点P.由(2)知,此时∠APB
最大,点P为最佳射门点.(或画出正确的示意图)------------5分
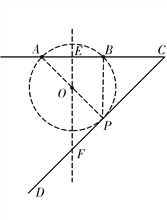 设⊙O的半径为r,连接OA,OP.
设⊙O的半径为r,连接OA,OP.
∵EF垂直平分AB,∠C=45°,AB=BC=![]() ∴EC=
∴EC=![]()
∴∠CFE=∠C=45°,EC=EF=![]() ∴CF=15------------6分
∴CF=15------------6分
∵⊙O与CD相切于点P,∴OP⊥CD.
∴OP=FP=r,OF=![]() r.
r.
∴OE=![]() -
-![]() r. ------------------------------------7分
r. ------------------------------------7分
在Rt△AOE中,AE2+OE2=OA2,
∴(![]() )2+(
)2+(![]() -
-![]() r)2=r2-----------------------------------8分
r)2=r2-----------------------------------8分
∴r=5或r=25(舍). ------------------------------------------9分
∴PF=5. ∴PC=FC-PF=10.--------------------------------10分

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】6月5日是世界环境日,某校组织了一次环保知识竞赛,每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将某年级的一班和二班的成绩整理并绘制成统计图. 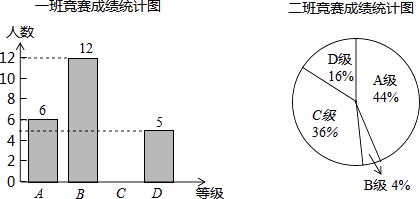
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(1)把一班竞赛成绩统计图补充完整;
(2)写出表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | a | b | 90 |
二班 | d | 80 | c |
(3)请从平均数和中位数方面比较一班和二班的成绩,对这次竞赛成绩的结果进行分析.

