题目内容
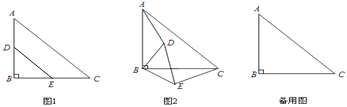
【题目】如图1,△DBE和△ABC都是等腰直角三角形,D,E两点分别在AB,BC上,∠B=90°.将△DBE绕点B顺时针旋转,得到图2.
(1)在图2中,求证:AD=CE;
(2)设AB= ![]() ,BD=
,BD= ![]() ,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和
,且当A、D、E三点在同一直线上时,∠EAC=30°,请利用备用图画出此情况下的图形,并求旋转的角度和![]() 的值.
的值.
【答案】(1)详见解析;(2)30°,![]() .
.
【解析】试题分析:由△DBE和△ABC都是等腰直角三角形,可得AB=BC, DB=BE,∠ABD=∠CBE,根据“SAS”可证△ABD≌△CBE,从而AD=CE;
(2)先证△ABD≌△CBE,可求∠ADB=∠CEB=135°,可求∠AEC=90°,进而求出∠BAD=45°-30°=15°,根据三角形内角和即可旋转角∠ABD的度数;由AE=AD+DE=cos30 ·AC,整理可得![]() 的值.
的值.
解:(1)∵△DBE和△ABC都是等腰直角三角形,
∴AB=BC, DB=BE,∠ABC=∠DBE=90°,∴∠ABD=90°-∠DBC=∠CBE=90°-∠DBC,
∴△ABD≌△CBE,
∴AD=CE;
(2)如图, A、D、E三点在同一直线上时,

∵△DBE和△ABC都是等腰直角三角形,
∴∠BAC=∠BDE=∠BED =45°,
又△ABD≌△CBE,∴∠ADB=∠CEB=135°.
∴∠AEC=90°,
∵∠EAC=30°,
∴∠BAD=45°-30°=15°,∴∠ABD=30°,即旋转角为30°.
∵△DBE和△ABC是等腰直角三角形,AB=![]() , BD=
, BD=![]() ,
,
∴AC=![]() ,DE=
,DE=![]() ,
,
∵△ABD≌△CBE,
∴AD=EC,
∵∠EAC=30°,∠AEC=90°,AC= ![]() ,
,
∴AD=EC=![]() ,
,
∴AE=AD+DE=![]() +
+![]() =
=![]() ,
,
整理得![]() .
.

【题目】某市居民使用自来水,每户每月水费按如下标准收费:月用水量不超过8立方米,按每立方米a元收取;月用水量超过8立方米但不超过14立方米的部分,按每立方米b元收取;月用水量超过14立方米的部分,按每立方米c元收取.下表是某月部分居民的用水量及缴纳水费的数据.
用水量(立方米) | 2.5 | 15 | 6 | 12 | 10.3 | 4.7 | 9 | 17 | 16 |
水费(元) | 5 | 33.4 | 12 | 25.6 | 21.52 | 9.4 | 18.4 | 39.4 | 36.4 |
(1) ①a= _____,b= _____,c= _____;
②若小明家七月份需缴水费31元,则小明家七月份用水 米3;
(2) 该市某用户两个月共用水30立方米,设该用户在其中一个月用水x立方米,请列式表示这两个月该用户应缴纳的水费.