题目内容
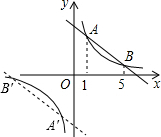 若直线y=k′x+b与双曲线y=
若直线y=k′x+b与双曲线y=| k″ |
| x |
| k″ |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:根据不等式与直线和双曲线解析式的关系,相当于把直线向下平移2b个单位,然后根据函数的对称性可得交点坐标与原直线的交点坐标关于原点对称,再找出直线在双曲线下方的自变量x的取值范围即可.
解答:解:由k′x<
+b,得k′x-b<
,
所以,不等式的解集可由双曲线不动,直线向下平移2b个单位得到,
直线向下平移2b个单位的图象如图所示,交点A′的横坐标为-1,交点B′的横坐标为-5,
当-5<x<-1或x>0时,双曲线图象在直线图象上方,
所以,不等式k′x<
+b的解集是-5<x<-1或x>0.
| k″ |
| x |
| k″ |
| x |
所以,不等式的解集可由双曲线不动,直线向下平移2b个单位得到,
直线向下平移2b个单位的图象如图所示,交点A′的横坐标为-1,交点B′的横坐标为-5,
当-5<x<-1或x>0时,双曲线图象在直线图象上方,
所以,不等式k′x<
| k″ |
| x |
点评:本题主要考查了反比例函数与一次函数的交点问题,根据不等式与函数解析式得出不等式的解集与双曲线和向下平移2b个单位的直线的交点有关是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,G、H是?ABCD对角线AC上的点,且AG=CH,E、F分别是AB、CD的中点.
如图,G、H是?ABCD对角线AC上的点,且AG=CH,E、F分别是AB、CD的中点.