题目内容
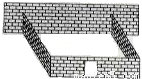
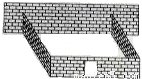
小亮家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形庭院,如图所示,现在已备足可以砌12米长的墙的材料.(1)如果想围成面积为16m2的矩形庭院,你能够教他们怎么围吗?
(2)如果想围成尽可能大得面积,能围多大?并给出设计方案.

【答案】分析:(1)根据长方形的面积公式列方程求解即可;
(2)利用配方法求出二次函数的最值即可.
解答:解:(1)设垂直于墙的边长为xm,
则x(12-2x)=16,
解得x1=2,x2=4,
当x=2时,12-2x=8,
当x=4时,12-2x=4,
所以垂直于墙的边长为2米或4米;(4分)
(2)函数可化为:y=x(12-2x)=-2x 2+12x=-2(x-3) 2+18,
因此当x=3时,最大面积为18(米2).
点评:本题考查了一元二次方程的应用,对于面积问题应熟记各种图形的面积公式.运用二次函数知识求最值问题,常常用公式法或配方法求解.注意自变量的取值范围.
(2)利用配方法求出二次函数的最值即可.
解答:解:(1)设垂直于墙的边长为xm,
则x(12-2x)=16,
解得x1=2,x2=4,
当x=2时,12-2x=8,
当x=4时,12-2x=4,
所以垂直于墙的边长为2米或4米;(4分)
(2)函数可化为:y=x(12-2x)=-2x 2+12x=-2(x-3) 2+18,
因此当x=3时,最大面积为18(米2).
点评:本题考查了一元二次方程的应用,对于面积问题应熟记各种图形的面积公式.运用二次函数知识求最值问题,常常用公式法或配方法求解.注意自变量的取值范围.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 26、小亮家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,现在已备足可以砌12米长的墙的材料.
26、小亮家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,现在已备足可以砌12米长的墙的材料. 小亮家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形庭院,如图所示,现在已备足可以砌12米长的墙的材料.
小亮家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形庭院,如图所示,现在已备足可以砌12米长的墙的材料.