题目内容
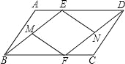
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
【答案】见解析
【解析】
试题分析:(1)根据平行四边形的性质和全等三角形的判定,在△ABE和△CDF中,很容易确定SAS,即证结论;
(2)在已知条件中求证全等三角形,即△ABE≌△CDF,△MBF≌△NDE,得两对边分别对应相等,根据平行四边形的判定,即证.
试题解析:(1)∵ABCD中,AB=CD,∠A=∠C,
又∵AE=CF,
∴△ABE≌△CDF;
(2)四边形MFNE平行四边形.
由(1)知△ABE≌△CDF,
∴BE=DF,∠ABE=∠CDF,
又∵ME=BM=![]() BE,NF=DN=
BE,NF=DN=![]() DF
DF
∴ME=NF=BM=DN,
又∵∠ABC=∠CDA,
∴∠MBF=∠NDE,又∵AD=BC,AE=CF,∴DE=BF,
∴△MBF≌△NDE,
∴MF=NE,
∴四边形MFNE是平行四边形.

练习册系列答案
相关题目