题目内容
某人用15元钱买了20张邮票，其中有1元，8角，2角的邮票．问他可能有多少种不同的买法？
解：设买一元邮票x张，8角邮票y张，2角邮票z张．
根据题意得：
由②得：5x+4y+z=75 ③
由③-①得：4x+3y=55，即
∵y＞0
∴
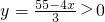
∴x的最大整数取13
经验证当x=1，4，7，10，13时，y取正整数
∴原方程组的正整数解为：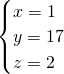
，
，
，
，
．
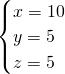所以共有5种不同的买法．
分析：首先假设一元邮票x张，8角邮票y张，2角邮票z张．
根据题意列出方程组
，通过加减消元法得到，利用本题隐含的条件x、y、z均为正整数，讨论x的取值，进而求得适合条件的y、z取值．
点评：此方程组称为不定方程组，即未知数的个数多于方程的个数，解决此类问题的关键是寻找隐含条件，尽量缩小未知数的取值范围．
根据题意得：
由②得：5x+4y+z=75 ③
由③-①得：4x+3y=55，即
∵y＞0
∴
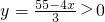
∴x的最大整数取13
经验证当x=1，4，7，10，13时，y取正整数
∴原方程组的正整数解为：
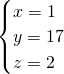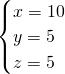，，，，．所以共有5种不同的买法．
分析：首先假设一元邮票x张，8角邮票y张，2角邮票z张．
根据题意列出方程组
，通过加减消元法得到，利用本题隐含的条件x、y、z均为正整数，讨论x的取值，进而求得适合条件的y、z取值．点评：此方程组称为不定方程组，即未知数的个数多于方程的个数，解决此类问题的关键是寻找隐含条件，尽量缩小未知数的取值范围．
练习册系列答案
名校课堂系列答案
相关题目