题目内容
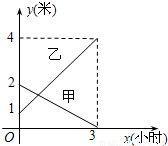
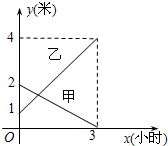 有甲乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲乙两个蓄水池中水的高度y(米)与注水时间x(小时)之间的函数图象如图所示,若要使甲乙两个蓄水池的蓄水量(指蓄水的体积)相同,则注水的时间应为
有甲乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲乙两个蓄水池中水的高度y(米)与注水时间x(小时)之间的函数图象如图所示,若要使甲乙两个蓄水池的蓄水量(指蓄水的体积)相同,则注水的时间应为1小时
1小时
.分析:先根据3小时后甲池的水为0求出甲池中的水量,然后根据乙池中水升高的高度3米求出每升高1米的水量,从而求出乙池中原有水量,再根据两蓄水池的蓄水体积相同列出方程求解即可.
解答:解:∵x=3时,甲池水量为0,
∴甲池原有水:6×3=18立方米,
3小时后乙池蓄水高度上升4-1=3米,
18÷3=6,
∴乙池中的水每升高1米,蓄水增加6立方米,
∵x=0时,乙池水高1米,
∴乙池原有水6立方米,
设x小时后甲、乙两池蓄水量(指蓄水的体积)相同,
则18-6x=6+6x,
解得x=1,
所以,注水的时间为1小时.
故答案为:1小时.
∴甲池原有水:6×3=18立方米,
3小时后乙池蓄水高度上升4-1=3米,
18÷3=6,
∴乙池中的水每升高1米,蓄水增加6立方米,
∵x=0时,乙池水高1米,
∴乙池原有水6立方米,
设x小时后甲、乙两池蓄水量(指蓄水的体积)相同,
则18-6x=6+6x,
解得x=1,
所以,注水的时间为1小时.
故答案为:1小时.
点评:本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.渗透了函数与方程的思想.

练习册系列答案
相关题目
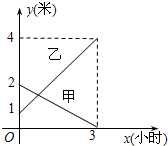 有甲乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲乙两个蓄水池中水的高度y(米)与注水时间x(小时)之间的函数图象如图所示,若要使甲乙两个蓄水池的蓄水量(指蓄水的体积)相同,则注水的时间应为________.
有甲乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲乙两个蓄水池中水的高度y(米)与注水时间x(小时)之间的函数图象如图所示,若要使甲乙两个蓄水池的蓄水量(指蓄水的体积)相同,则注水的时间应为________.