题目内容
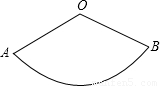
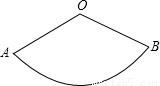
如图,扇形OAB的圆心角度数为n,OA=3,AB的长度为2π.(1)求n的值;
(2)将此扇形围成一个圆锥,使扇形的两条半径OA与OB重合,画出此圆锥的正视图并求出该正视图的周长.(正视图只须画示意图)

【答案】分析:(1)根据弧长公式可得到关于n的方程,解方程即可;
(2)根据圆锥的底面圆的周长等于其展开的扇形的弧长得求出圆锥的底面圆的半径,再根据圆锥的正视图为等腰三角形,其腰长为扇形的半径,底边长为底面圆的直径可得到圆锥的正视图的周长.
解答: 解:(1)∵扇形OAB的圆心角度数为n,OA=3,AB的长度为2π.
解:(1)∵扇形OAB的圆心角度数为n,OA=3,AB的长度为2π.
∴2π= ,
,
∴n=120°;
(2)设圆锥的底面圆的半径为r
∴2π•r=2π,
∴r=1,
又∵圆锥的正视图为等腰三角形,其腰长为扇形的半径,底边长为底面圆的直径,
∴圆锥的正视图的周长=3+3+2=8.
圆锥的正视图(正视图为等腰三角形,底边长等于圆锥底面圆的直径,腰长等于母线长,如图.
点评:本题考查了弧长公式:l=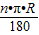 ,圆锥的有关计算:圆锥的底面圆的周长等于其展开的扇形的弧长,母线长等于扇形的半径;也考查了圆锥的正视图的画法.
,圆锥的有关计算:圆锥的底面圆的周长等于其展开的扇形的弧长,母线长等于扇形的半径;也考查了圆锥的正视图的画法.
(2)根据圆锥的底面圆的周长等于其展开的扇形的弧长得求出圆锥的底面圆的半径,再根据圆锥的正视图为等腰三角形,其腰长为扇形的半径,底边长为底面圆的直径可得到圆锥的正视图的周长.
解答:
 解:(1)∵扇形OAB的圆心角度数为n,OA=3,AB的长度为2π.
解:(1)∵扇形OAB的圆心角度数为n,OA=3,AB的长度为2π.∴2π=
 ,
,∴n=120°;
(2)设圆锥的底面圆的半径为r
∴2π•r=2π,
∴r=1,
又∵圆锥的正视图为等腰三角形,其腰长为扇形的半径,底边长为底面圆的直径,
∴圆锥的正视图的周长=3+3+2=8.
圆锥的正视图(正视图为等腰三角形,底边长等于圆锥底面圆的直径,腰长等于母线长,如图.
点评:本题考查了弧长公式:l=
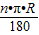 ,圆锥的有关计算:圆锥的底面圆的周长等于其展开的扇形的弧长,母线长等于扇形的半径;也考查了圆锥的正视图的画法.
,圆锥的有关计算:圆锥的底面圆的周长等于其展开的扇形的弧长,母线长等于扇形的半径;也考查了圆锥的正视图的画法. 
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
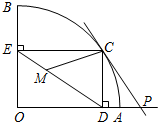 如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=r,圆心角∠AOB=90°,点C是
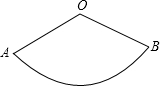 (2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,
(2012•珠海三模)如图:扇形OAB的圆心角∠AOB=120°,半径OA=6cm,