Question

【题目】在平面直角坐标系中，A（2，0）、B（0，3），过点B作直线l∥x轴，点P（a，3）是直线上的动点，以AP为边在AP右侧作等腰RtAPQ，∠APQ=90°，直线AQ交y轴于点C．

(1)当a=时，求点Q的坐标；

(2)当PA+PO最小时，求a.

Answer 1

【答案】(1)（4.5，3.5）；(2)a=1

【解析】试题分析：（1）要求点Q的坐标，可作QF⊥BP，由于BP、OB已知，只需求出PF和QF．从条件“△APQ为等腰直角三角形”出发，构造全等，即可解决问题．

（2）本题要求动点P到两定点A、O的距离之和AP+OP的最小值，只需找到点O关于直线l的对称点M，连接AM，AM与直线l的交点即为满足条件的点P，就可求出a的值．

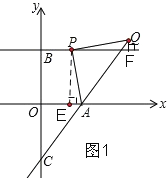
试题解析：（1）过点P作PE⊥OA，垂足为E，过点Q作QF⊥BP，垂足为F，如图1，

∵BP∥OA，PE⊥OA，∴∠EPF=∠PEO=90°，

∵∠APQ=90°，∴∠EPA=∠FPQ=90°-∠APF，

在△PEA和△PFQ中， ，∴△PEA≌△PFQ，

∴PE=PF，EA=QF，

∵a=1，∴P（1，3），∴OE=BP=1，PE=3，

∵A（2，0），∴OA=2，∴EA=1，∴PF=3，QF=1，

∴点Q的坐标为（4，4）；

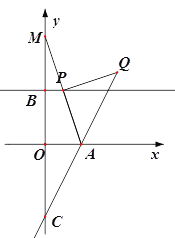
（2）如图，作点O关于直线l 的对称点M，连接AM，交直线l于点P，则此时OP+OA的值最小，

由题意易用得点M的坐标为（0，6），

设直线AM的解析式为y=kx+b，

则有 ，解得 ，所以直线AM的解析式为：y=-3x+6，

当y=3时，3=-3x+6，解得x=1，所以点P坐标为（1，3），所以a=1.