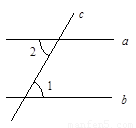Question

23、已知以下基本事实：①对顶角相等；②一条直线截两条平行直线所得的同位角相等；③两条直线被第三条直线所截，若同位角相等，则这两条直线平行；④全等三角形的对应边、对应角分别相等．
（1）在利用以上基本事实作为依据来证明命题“两直线平行，内错角相等”时，必须要用的基本事实有

①②

（填入序号即可）；
（2）根据在（1）中的选择，结合所给图形，请你证明命题“两直线平行，内错角相等”．
已知：如图，

a∥b，直线a、b被直线c所截

．
求证：

∠1=∠2

．
证明：

∵a∥b，
∴∠1=∠3（两直线平行，同位角相等）．
∵∠3=∠2（对顶角相等），
∴∠1=∠2（等量代换）

．

Answer 1

分析：（1）利用图示：根据平行线的性质，证明“两直线平行，内错角相等”的过程解答；
（2）根据“两直线a∥b，判定同位角∠1=∠3”，然后由对顶角∠3=∠2及等量代换证得∠1=∠2．

解答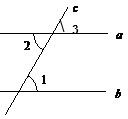：解：（1）①②；（2分）

（2）已知：a∥b，直线a、b被直线c所截．
求证：∠1=∠2．（4分）
∵a∥b，
∴∠1=∠3（两直线平行，同位角相等）．（6分）
∵∠3=∠2（对顶角相等），
∴∠1=∠2（等量代换）．（8分）
故答案为：
（1）①②；
（2）a∥b，直线a、b被直线c所截；
a∥b，直线a、b被直线c所截；
∵a∥b，
∴∠1=∠3（两直线平行，同位角相等）．（6分）
∵∠3=∠2（对顶角相等），
∴∠1=∠2（等量代换）．

点评：本题考查了平行线的性质．解答此题时，利用了平行线的性质：两直线平行，同位角相等，对顶角相等及等量代换的知识．