题目内容
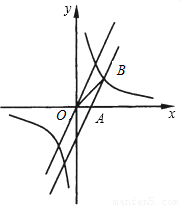
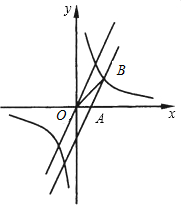 如图,将直线y=2x沿y轴向下平移后,得到的直线与x轴交于点A(
如图,将直线y=2x沿y轴向下平移后,得到的直线与x轴交于点A(| 5 |
| 2 |
| k |
| x |
| 15 |
| 4 |
(1)求直线AB的解析式;
(2)求双曲线的解析式.
分析:(1)设直线AB的解析式为y=2x-b,把A(
,0)代入此解析式即可求出d的值,进而求出直线AB的解析式;
(2)作BD⊥x轴,由△OAB的面积
可求出BD的长,再根据B点在直线y=2x-5上可求出x的值,进而求出B点坐标,由点坐标即可求出k的值,进而求出反比例函数的解析式.
| 5 |
| 2 |
(2)作BD⊥x轴,由△OAB的面积
| 15 |
| 4 |
解答: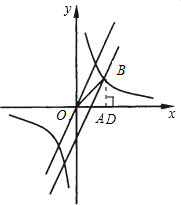 解:(1)直线AB的解析式为y=2x-b,把A(
解:(1)直线AB的解析式为y=2x-b,把A(
,0)代入得,
0=2×
-b,
解得b=5,
故此直线的解析式为:y=2x-5;
(2)作BD⊥x轴,
∵△OAB的面积
,即
OA•BD=
,
∵A(
,0),
∴BD=3,
∵B点在直线y=2x-5上,
∴3=2x-5,解得x=4,
∴B(4,3)
∵B点在反比例函数y=
上,
∴k=3×4=12,
∴此反比例函数的解析式为:y=
.
 解:(1)直线AB的解析式为y=2x-b,把A(
解:(1)直线AB的解析式为y=2x-b,把A(| 5 |
| 2 |
0=2×
| 5 |
| 2 |
解得b=5,
故此直线的解析式为:y=2x-5;
(2)作BD⊥x轴,
∵△OAB的面积
| 15 |
| 4 |
| 1 |
| 2 |
| 15 |
| 4 |
∵A(
| 5 |
| 2 |
∴BD=3,
∵B点在直线y=2x-5上,
∴3=2x-5,解得x=4,
∴B(4,3)
∵B点在反比例函数y=
| k |
| x |
∴k=3×4=12,
∴此反比例函数的解析式为:y=
| 12 |
| x |
点评:本题考查的是用待定系数法求一次函数的解析式及反比例函数系数k的几何意义,熟知以上知识是解答此题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
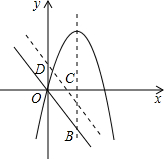 如图,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点.若点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,且以CD为直角边的△PCD与△OCD相似,则点P的坐标为
如图,将直线y=-2x沿y轴向上平移,分别交x轴、y轴于C、D两点.若点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,且以CD为直角边的△PCD与△OCD相似,则点P的坐标为 如图,将直线y=2x沿y轴向下平移后,得到的直线与x轴交于点
如图,将直线y=2x沿y轴向下平移后,得到的直线与x轴交于点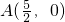 ,与双曲线
,与双曲线 在第一象限交于点B,且△OAB的面积
在第一象限交于点B,且△OAB的面积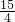 .
. ,与双曲线
,与双曲线 在第一象限交于点B,且△OAB的面积
在第一象限交于点B,且△OAB的面积 .
.
 ,与双曲线
,与双曲线 在第一象限交于点B,且△OAB的面积
在第一象限交于点B,且△OAB的面积 .
.