题目内容
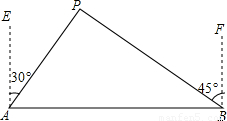
（2009•中山）如图所示，A、B两城市相距100km，现计划在这两座城市间修建一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上，已知森林保护区的范围在以P点为圆心，50km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：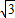
≈1.732，
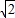≈1．414）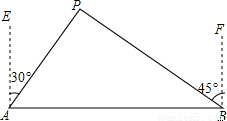
【答案】分析：过点P作PC⊥AB，C是垂足．AC与BC就都可以根据三角函数用PC表示出来．根据AB的长，得到一个关于PC的方程，解出PC的长．从而判断出这条高速公路会不会穿越保护区．
解答：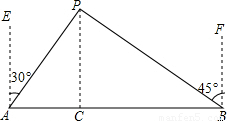
解：过点P作PC⊥AB，C是垂足．
则∠APC=30°，∠BPC=45°，
AC=PC•tan30°，BC=PC•tan45°．
∵AC+BC=AB，
∴PC•tan30°+PC•tan45°=100km，
∴
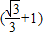PC=100，
∴PC=50（3-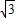
）≈50×（3-1.732）≈63.4km＞50km．
答：森林保护区的中心与直线AB的距离大于保护区的半径，所以计划修筑的这条高速公路不会穿越保护区．
点评：解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
解答：
解：过点P作PC⊥AB，C是垂足．则∠APC=30°，∠BPC=45°，
AC=PC•tan30°，BC=PC•tan45°．
∵AC+BC=AB，
∴PC•tan30°+PC•tan45°=100km，
∴
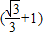PC=100，∴PC=50（3-
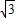）≈50×（3-1.732）≈63.4km＞50km．答：森林保护区的中心与直线AB的距离大于保护区的半径，所以计划修筑的这条高速公路不会穿越保护区．
点评：解一般三角形的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
阅读快车系列答案
相关题目
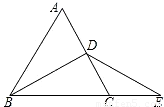
≈1.732，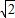
≈1．414）
