Question

（2012•湖里区一模）如图，在四边形ABCD中，∠B=∠D=90°，AB、BC的长为关于x的一元二次方程x2-4

10

x+

1

4

m²-m+41=0的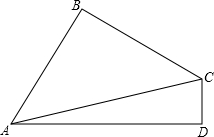两根．
（1）求AC的长；
（2）若四边形ABCD的面积为36，求△ACD的周长．

Answer 1

分析：（1）由判别式及非负数的性质可求m的值，再利用勾股定理即可求出AC的长；
（2）因为四边形ABCD的面积=三角形ABCD的面积+三角形ADC的面积，由（1）可以求出三角形ABC的面积，所以三角形ADC的面积可以求出，进而得到AD和CD的数量关系，再利用勾股定理即可求出AD+BC的值，所以三角形ACD的周长可求出．

解答：解：（1）∵AB、BC的长为关于x的一元二次方程x2-4

10

x+

1

4

m²-m+41=0的两根．
∴△=（-4

10

）²-4×（

1

4

m²-m+41）≥0，
即-（m-2）²≥0，
∴m-2=0，
∴m=2，
∴原方程为x2-4

10

x+40=0．
解方程得：x=2

10

，
∴AB=BC=2

10

，
∵∠B=90°，
∴在Rt△ABC中，AC=

AB2+BC2

=4

5

；

（2）∵四边形ABCD的面积=△ABC的面积+△ADC的面积，S_△ABC=

1

2

AB•BC=20，
∴S_△ADC=36-20=16，
∴

1

2

AD•CD=16，
∴AD•CD=32，
∵∠D=90°，
∴AD²+CD²=AC²=80，
∴AD+CD=12，
∴△ACD的周长=AD+CD+AC=12+4

5

．

点评：本题考查了一元二次方程根的判别式和非负数的性质、勾股定理的运用和三角形的面积公式以及求三角形的周长，属于基础性题目．