题目内容
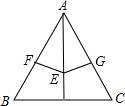在等腰三角形ABC中，AB=AC，AD是△ABC底边BC上的高线，E为AD上任意一点，且EF⊥AB于E，EG⊥AC于G，请你说明EF=EG的理由．
证明：∵AB=AC，AD是△ABC底边BC上的高线，
∴AD是∠BAC的平分线，
∵EF⊥AB于E，EG⊥AC于G，
∴EF=EG．
分析：由已知条件，根据等腰三角形的性质可证AD是∠BAC的平分线，再根据角平分线的性质可证EF=EG．
点评：本题考查了等腰三角形的性质和平分线的性质，即角平分线上的点到角两边的距离相等．得到高线AD是三角形顶角的平分线是正确解答本题的关键．
∴AD是∠BAC的平分线，
∵EF⊥AB于E，EG⊥AC于G，
∴EF=EG．
分析：由已知条件，根据等腰三角形的性质可证AD是∠BAC的平分线，再根据角平分线的性质可证EF=EG．
点评：本题考查了等腰三角形的性质和平分线的性质，即角平分线上的点到角两边的距离相等．得到高线AD是三角形顶角的平分线是正确解答本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
如图：在等腰三角形ABC中，AB=AC，∠A=40°，则∠B=
在等腰三角形ABC中，∠C=90°，BC=2cm．如果以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，那么点B′与点B的原来位置相距
如图所示，在等腰三角形ABC中，AB=AC=13cm，底边BC=10cm，求底边上的高AD和△ABC的面积．
如图，在等腰三角形ABC中，两底角的平分线BE和CD相交于点0，则△OBC是