题目内容
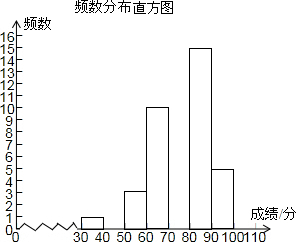
某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
频数分布表
| 成绩分组 | 频数 | 频率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | 0.06 |
| 60≤x<70 | 10 | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合计 | 50 | 1 |
(2)补全频数分布表和频数分布直方图;
(3)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
【答案】分析:(1)观察每个分组的起末数据,即可得出答案;
(2)总的调查学生为50人,根据第三组的频数为3,即可求出该组的频率;根据第四组的频率,可求出该组的频数;继而即可补全频数分布表和频数分布直方图即可;
(3)用总人数乘以第五组和第六组的频率,计算即可得解.
解答:解:(1)以上分组的组距=10;
(2)∵总的调查学生为50人,第三组的频数为3,
∴该组的频率=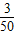 =0.06,
=0.06,
∵第四组的频率为0.2,
∴该组的频数=0.2×50=10,
补全频数分布表如下所示:
补全频数分布直方图如下所示:
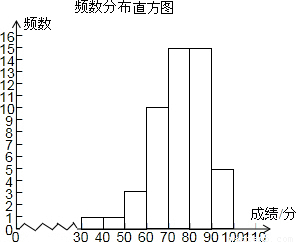
(3)该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数为:300×(0.1+0.3)=120(人).
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
(2)总的调查学生为50人,根据第三组的频数为3,即可求出该组的频率;根据第四组的频率,可求出该组的频数;继而即可补全频数分布表和频数分布直方图即可;
(3)用总人数乘以第五组和第六组的频率,计算即可得解.
解答:解:(1)以上分组的组距=10;
(2)∵总的调查学生为50人,第三组的频数为3,
∴该组的频率=
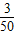 =0.06,
=0.06,∵第四组的频率为0.2,
∴该组的频数=0.2×50=10,
补全频数分布表如下所示:
| 成绩分组 | 频数 | 频率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | 0.06 |
| 60≤x<70 | 10 | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合计 | 50 | 1 |

(3)该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数为:300×(0.1+0.3)=120(人).
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.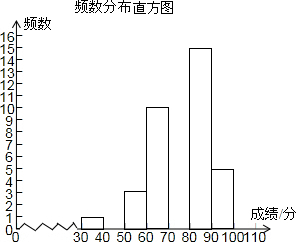
频数分布表
| 成绩分组 | 频 数 | 频 率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | |
| 60≤x<70 | | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合 计 | 50 | 1 |
(2)补全频数分布表和频数分布直方图;
(3)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
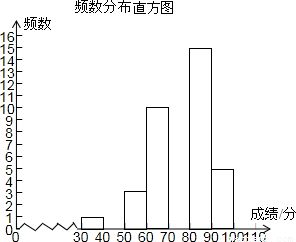
频数分布表
|
成绩分组 |
频 数 |
频 率 |
|
30≤x<40 |
1 |
0.02 |
|
40≤x<50 |
1 |
0.02 |
|
50≤x<60 |
3 |
|
|
60≤x<70 |
|
0.2 |
|
70≤x<80 |
15 |
0.3 |
|
80≤x<90 |
15 |
0.3 |
|
90≤x<100 |
5 |
0.1 |
|
合 计 |
50 |
1 |
(1)以上分组的组距= ;
(2)补全频数分布表和频数分布直方图;
(3)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.