题目内容
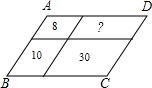
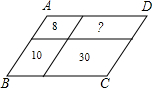 如图,把平行四边形ABCD分成4个平行四边形,已知其中三个面积分别为8、10、30,则第四个平行四边形的面积是( )
如图,把平行四边形ABCD分成4个平行四边形,已知其中三个面积分别为8、10、30,则第四个平行四边形的面积是( )| A、28 | B、26 | C、24 | D、22 |
分析:由平行四边形ABCD被分成4个平行四边形,易得四边形AMOE与四边形MBFO同高,底分别为OE与OF,四边形EOND与四边形OFCN同高,底分别为OE与OF,即可得四边形AMOE与四边形MBFO面积的比等于对应底的比,四边形EOND与四边形OFCN等于对应底的比,然后由其中三个面积分别为8、10、30,根据比例的性质,即可求得第四个平行四边形的面积.
解答: 解:∵平行四边形ABCD被分成4个平行四边形,
解:∵平行四边形ABCD被分成4个平行四边形,
∴AB∥EF∥CD,AD∥MN∥BC,
∴四边形AMOE与四边形MBFO同高,底分别为OE与OF,四边形EOND与四边形OFCN同高,底分别为OE与OF,
∴
=
=
=
,
∴
=
,
即:
=
,
∴S四边形EOND=24.
故选C.
 解:∵平行四边形ABCD被分成4个平行四边形,
解:∵平行四边形ABCD被分成4个平行四边形,∴AB∥EF∥CD,AD∥MN∥BC,
∴四边形AMOE与四边形MBFO同高,底分别为OE与OF,四边形EOND与四边形OFCN同高,底分别为OE与OF,
∴
| S四边形AEMO |
| S四边形MBFO |
| OE |
| OF |
| 8 |
| 10 |
| 4 |
| 5 |
∴
| S四边形EOND |
| S四边形OFCN |
| OE |
| OF |
即:
| S四边形EOND |
| 30 |
| 4 |
| 5 |
∴S四边形EOND=24.
故选C.
点评:此题考查了平行线的性质.此题难度适中,解题的关键是抓住四边形AMOE与四边形MBFO面积的比等于对应底的比,四边形EOND与四边形OFCN等于对应底的比,且比为OE:OF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
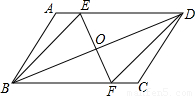
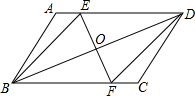 如图,把平行四边形ABCD翻折,使B点与D点重合,EF为折痕,连接BE,DF.请你猜一猜四边形BFDE是什么特殊四边形?并证明你的猜想.
如图,把平行四边形ABCD翻折,使B点与D点重合,EF为折痕,连接BE,DF.请你猜一猜四边形BFDE是什么特殊四边形?并证明你的猜想.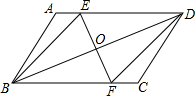 如图,把平行四边形ABCD翻折,使B点与D点重合,EF为折痕,连接BE,DF.请你猜一猜四边形BFDE是什么特殊四边形?并证明你的猜想.
如图,把平行四边形ABCD翻折,使B点与D点重合,EF为折痕,连接BE,DF.请你猜一猜四边形BFDE是什么特殊四边形?并证明你的猜想.