Question

已知坐标原点O和点A（1，1），试在X轴上找到一点P，使△AOP为等腰三角形，写出满足条件的点P的坐标            

Answer 1

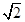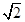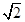（1，0）、（2，0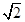）、（，0）、（-，0）．

试题分析：先画出坐标系，由于OA=AB=1，故可知△OAB就是等腰三角形，从而有点B的坐标；以A为圆心，OA长为半径画弧，与x轴交点是C，故△AOC是等腰三角形，C点就是所求；也可考虑以O为圆心，OA长为半径画弧，与x轴有两个交点E、F，也是所求．
如图：

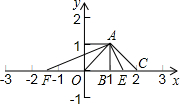
①连接OA，由于OA=AB=1，
∴△OAB就是等腰三角形，且B的坐标是（1，0）；
②以A为圆心，OA长为半径画弧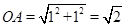，，与x轴交于点C，
∴△AOC是等腰三角形，且C点的坐标是（2，0）；
③以O为圆心，OA长为半径画弧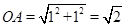，，分别交x轴与E、F，且E点坐标是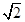（，0），F点坐标是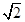（-，0）．
故答案为：（1，0）、（2，0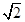）、（，0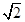）、（-，0）．