题目内容
二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac-b2＜0；②4a+c＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠-1），
其中正确结论的个数是（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一个不透明的袋子里有若干个小球，它们除了颜色外，其它都相同，甲同学从袋子里随机摸出一个球，记下颜色后放回袋子里，摇匀后再次随机摸出一个球，记下颜色，…，甲同学反复大量实验后，根据白球出现的频率绘制了如图所示的统计图，则下列说法正确的是（ ）| A、袋子一定有三个白球 | B、袋子中白球占小球总数的十分之三 | C、再摸三次球，一定有一次是白球 | D、再摸1000次，摸出白球的次数会接近330次 |
如图，已知抛物线y1=-2x2+2，直线y2=2x+2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．下列给出四个说法：二次函数y=ax2-2x-3（a＜0）的图象一定不经过（ ）
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限． |
如图，是抛物线y=ax2+bx+c（a≠0）图象的一部分．已知抛物线的对称轴为x=2，与x轴的一个交点是（-1，0）．有下列结论：①abc＞0；②4a-2b+c＜0；③4a+b=0；④抛物线与x轴的另一个交点是（5，0）；⑤点（-3，y1），（6，y2）都在抛物线上，则有y1＜y2．
其中正确的是（ ）
| A、①②③ | B、②④⑤ | C、①③④ | D、③④⑤ |
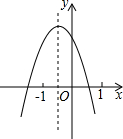已知二次函数y=ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2-4ac＞0；③3a+c＞0；④（a+c）2＜b2，
其中正确的结论有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论：①ac＞0；
②a-b+c＜0；
③当x＜0时，y＜0；
④9a+3b+c＞0；
⑤方程ax2+bx+c=0（a≠0）有两个大于-1的实数根．
其中正确的结论有（ ）
| A、4个 | B、3个 | C、2个 | D、1个 |
已知抛物线y=ax2+bx+c的开口向下，且经过点（1，2），与x轴交点的横坐标分别为x1，x2，其中-1＜x1＜0，1＜x2＜2，下列结论：要使抛物线y=3x2-6x+1平移后经过点（1，4），则可以将此抛物线（ ）
| A、向下平移2个单位 | B、向上平移6个单位 | C、向右平移1个单位 | D、向左平移2个单位 |