题目内容
 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面 的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点o为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面 的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点o为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
(1)求该抛物线的解析式;
(2)如果身高为157.5厘米的小明站在OD之间且离点O的距离为t米,绳子甩到最高处时超过他的头顶,请结合函数图象,求出t的取值范围.
解:(1)由题意得点E(1,1.4),B(6,0.9),
代入y=ax2+bx+0.9,得: ,
,
解得: .
.
故所求的抛物线的解析式为:y=-0.1x2+0.6x+0.9;
(2)157.5cm=1.575m,
当y=1.575时,-0.1x2+0.6x+0.9=1.575,
解得:x1= ,x2=
,x2= ,
,
则 <t<
<t< .
.
分析:(1)已知抛物线解析式y=ax2+bx+0.9,选定抛物线上两点E(1,1.4),B(6,0.9)坐标代入即可得出a、b的值,继而得出抛物线解析式;
(2)求出y=1.575时,对应的x的两个值,从而可确定t的取值范围.
点评:本题考查了二次函数的应用及坐标的求法,此题为数学建模题,解答本题的关键是注意审题,将实际问题转化为求函数最值问题,培养自己利用数学知识解答实际问题的能力.
代入y=ax2+bx+0.9,得:
 ,
,解得:
 .
.故所求的抛物线的解析式为:y=-0.1x2+0.6x+0.9;
(2)157.5cm=1.575m,
当y=1.575时,-0.1x2+0.6x+0.9=1.575,
解得:x1=
 ,x2=
,x2= ,
,则
 <t<
<t< .
.分析:(1)已知抛物线解析式y=ax2+bx+0.9,选定抛物线上两点E(1,1.4),B(6,0.9)坐标代入即可得出a、b的值,继而得出抛物线解析式;
(2)求出y=1.575时,对应的x的两个值,从而可确定t的取值范围.
点评:本题考查了二次函数的应用及坐标的求法,此题为数学建模题,解答本题的关键是注意审题,将实际问题转化为求函数最值问题,培养自己利用数学知识解答实际问题的能力.

练习册系列答案
相关题目
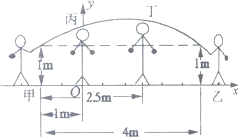 你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似地看为抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距离为4m,距地面均为1m,学生丙、丁分别站在距甲拿绳的手水平距离1m、2.5m处,绳子在甩到最高处时刚好通过他们的头顶.已知学生丙的身高1.5m,则学生丁的身高为
你知道吗?平时我们在跳绳时,绳甩到最高处的形状可近似地看为抛物线,如图,正在甩绳的甲、乙两名学生拿绳的手间距离为4m,距地面均为1m,学生丙、丁分别站在距甲拿绳的手水平距离1m、2.5m处,绳子在甩到最高处时刚好通过他们的头顶.已知学生丙的身高1.5m,则学生丁的身高为 顶,请结合图象,写出t的取值范围
顶,请结合图象,写出t的取值范围